题目内容
9.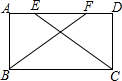 已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.
已知,如图,在矩形ABCD中,点E,F在边AD上,且AE=DF,求证:BF=CE.
分析 由矩形的性质得出∠A=∠D=90°,AB=DC,再证出AF=DE,由SAS证明△ABF≌△DCE,得出对应边相等即可.
解答 证明:∵四边形ABCD是矩形,
∴∠A=∠D=90°,AB=DC,
∵AE=DF,
∴AF=DE,
在△ABF和△DCE中,$\left\{\begin{array}{l}{AB=DC}\\{∠A=∠D}&\\{AF=DE}\end{array}\right.$,
∴△ABF≌△DCE(SAS),
∴BF=CE.
点评 本题考查了矩形的性质、全等三角形的判定与性质;熟练掌握矩形的性质,证明三角形全等是解决问题的关键.

练习册系列答案
相关题目
19.泉州市丰泽区某校初三1班五位同学的身高(单位:cm)组成一组数据为:170、168、165、172、165,则这五位同学身高的中位数是( )
| A. | 165 | B. | 168 | C. | 170 | D. | 172 |
20.两个相似多边形的面积之比为1:9,则它们的周长之比为( )
| A. | 1:3 | B. | 1:9 | C. | 1:$\sqrt{3}$ | D. | 2:3 |
14.甲、乙两人在100米直道AB上练习匀速往返跑,若甲、乙分别中A,B两端同时出发,分别到另一端点处掉头,掉头时间不计,速度分别为5m/s和4m/s.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);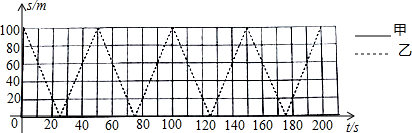
(2)根据(1)中所画图象,完成下列表格:
(3)①直接写出甲、乙两人分别在第一个100m内,s与t的函数解析式,并指出自变量t的取值范围;
②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离.
(1)在坐标系中,虚线表示乙离A端的距离s(单位:m)与运动时间t(单位:s)之间的函数图象(0≤t≤200),请在同一坐标系中用实线画出甲离A端的距离s与运动时间t之间的函数图象(0≤t≤200);

(2)根据(1)中所画图象,完成下列表格:
| 两人相遇次数 (单位:次) | 1 | 2 | 3 | 4 | … | n |
| 两人所跑路程之和 (单位:m) | 100 | 300 | 500 | 700 | … | 200n-100 |
②当t=390s时,他们此时相遇吗?若相遇,应是第几次?若不相遇,请通过计算说明理由,并求出此时甲离A端的距离.
1.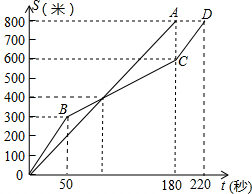 在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
 在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )
在一次800米的长跑比赛中,甲、乙两人所跑的路程s(米)与各自所用时间t(秒)之间的函数图象分别为线段OA和折线OBCD,则下列说法正确的是( )| A. | 甲的速度随时间的增加而增大 | B. | 乙的平均速度比甲的平均速度大 | ||
| C. | 在起跑后第180秒时,两人相遇 | D. | 在起跑后第50秒时,乙在甲的前面 |
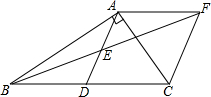 在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.
在Rt△ABC中,∠BAC=90°,D是BC的中点,E是AD的中点,过点A作AF∥BC交BE的延长线于点F.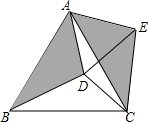 如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.
如图,在等边△ABC内有一点D,AD=5,BD=6,CD=4,将△ABD绕A点逆时针旋转,使AB与AC重合,点D旋转至点E,则∠CDE的正切值为3$\sqrt{7}$.