题目内容
13.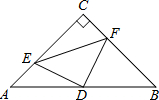 如图,在△ABC中,∠C=90°,AC=BC=5,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF,在此运动变化的过程中,△CEF周长的最小值是5+$\frac{5\sqrt{2}}{2}$.
如图,在△ABC中,∠C=90°,AC=BC=5,D是AB的中点,点E、F分别在AC、BC边上运动(点E不与点A、C重合),且保持AE=CF,连接DE、DF、EF,在此运动变化的过程中,△CEF周长的最小值是5+$\frac{5\sqrt{2}}{2}$.
分析 连接CD,由SAS定理可证△CDF和△ADE全等,从而可证∠EDF=90°,DE=DF.所以△DFE是等腰直角三角形;当E、F分别为AC、BC中点时,EF取最小值,根据三角形的中位线的性质得到EF,于是得到结论.
解答 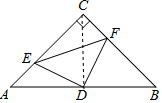 解:连接CD;
解:连接CD;
∵△ABC是等腰直角三角形,
∴∠DCB=∠A=45°,CD=AD=DB;
在△ADE与△CFD中,$\left\{\begin{array}{l}{AE=CF}\\{∠A=∠DCF}\\{AD=CD}\end{array}\right.$,
∴△ADE≌△CDF(SAS);
∴ED=DF,∠CDF=∠EDA;
∵∠ADE+∠EDC=90°,
∴∠EDC+∠CDF=∠EDF=90°,
∴△DFE是等腰直角三角形,
∵∠C=90°,AC=BC=5,
∴AB=5$\sqrt{2}$,
∴当,△CEF周长的最小时,EF取最小值,
∴E、F分别为AC、BC中点时,EF的值最小,
∴EF=$\frac{1}{2}$AB=$\frac{5\sqrt{2}}{2}$,
∴△CEF周长的最小值=CE+CF+EF=AE+CE+EF=AC+EF=5+$\frac{5\sqrt{2}}{2}$;
故答案为:5+$\frac{5\sqrt{2}}{2}$.
点评 此题主要考查了全等三角形的判定与性质,等腰三角形、直角三角形性质等知识,找到EF∥BC时取最小值是解题关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.甲班、乙班两班为举办“浓情‘苹’安夜”联欢活动,分别选派班委成员到集市上购买苹果,苹果的价格如下:
(1)甲班分两次共购买苹果70kg(第二次多于第一次),共付出255元;乙班一次购买苹果70kg.
①乙班买苹果付了210元;
②乙班比甲班少付了45元;
③甲班第一次、第二次分别购买苹果多少千克?请写出计算过程.
(2)若甲班分两次购买苹果70kg(第二次多于第一次),并且第一次购买不少于10kg,如何购买最省钱?最省的钱是多少?请直接写出最省钱的购买方案.
| 购买苹果数 | 不超过30kg | 30kg以上 且不超过50kg | 50kg以上 |
| 每千克价格 | 4元 | 3.5元 | 3元 |
①乙班买苹果付了210元;
②乙班比甲班少付了45元;
③甲班第一次、第二次分别购买苹果多少千克?请写出计算过程.
(2)若甲班分两次购买苹果70kg(第二次多于第一次),并且第一次购买不少于10kg,如何购买最省钱?最省的钱是多少?请直接写出最省钱的购买方案.
3.一元二次方程x2-2x=0的根是( )
| A. | x1=0,x2=2 | B. | x1=1,x2=2 | C. | x1=1,x2=-2 | D. | x1=0,x2=-2 |
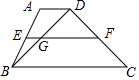 如图,梯形ABCD中,AD∥BC,对角线BD与中位线EF交于点G,若AD=2,EF=5,那么FG=4.
如图,梯形ABCD中,AD∥BC,对角线BD与中位线EF交于点G,若AD=2,EF=5,那么FG=4.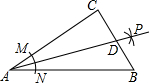 如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是30.
如图,在Rt△ABC中,∠C=90°,以顶点A为圆心,适当长为半径画弧,分别交AC,AB于点M、N,再分别以点M、N为圆心,大于$\frac{1}{2}$MN的长为半径画弧,两弧交于点P,作射线AB交边BC于点D,若CD=4,AB=15,则△ABD的面积是30.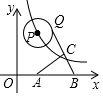 如图,动点P在函数y=$\frac{16}{x}$(x>0)的图象上移动,⊙P半径为2,A(3,0),B(6,0),点Q是⊙P上的动点,点C是QB的中点,则AC的最小值是2$\sqrt{2}$-1.
如图,动点P在函数y=$\frac{16}{x}$(x>0)的图象上移动,⊙P半径为2,A(3,0),B(6,0),点Q是⊙P上的动点,点C是QB的中点,则AC的最小值是2$\sqrt{2}$-1.