题目内容
18．
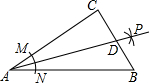如图，在Rt△ABC中，∠C=90°，以顶点A为圆心，适当长为半径画弧，分别交AC，AB于点M、N，再分别以点M、N为圆心，大于$\frac{1}{2}$MN的长为半径画弧，两弧交于点P，作射线AB交边BC于点D，若CD=4，AB=15，则△ABD的面积是30．
分析 根据角平分线的性质得到DE=DC=4，根据三角形的面积公式计算即可．
解答 
解：作DE⊥AB于E，
由基本尺规作图可知，AD是△ABC的角平分线，
∵∠C=90°，DE⊥AB，
∴DE=DC=4，
∴△ABD的面积=$\frac{1}{2}$×AB×DE=30，
故答案为：30．
点评 本题考查的是角平分线的性质、基本作图，掌握角的平分线上的点到角的两边的距离相等是解题的关键．
练习册系列答案
鸿图图书寒假作业假期作业吉林大学出版社系列答案
相关题目
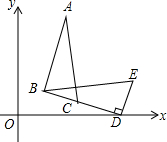如图，在△BDE中，∠BDE=90°，BD=3$\sqrt{2}$，点D的坐标是（5，0），∠BDO=15°，将△BDE旋转得到△ABC的位置，点C在BD上，则过A、B、D三点圆的圆心坐标为（$\frac{7}{2}$，$\frac{3}{2}$$\sqrt{3}$）．
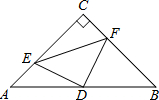如图，在△ABC中，∠C=90°，AC=BC=5，D是AB的中点，点E、F分别在AC、BC边上运动（点E不与点A、C重合），且保持AE=CF，连接DE、DF、EF，在此运动变化的过程中，△CEF周长的最小值是5+$\frac{5\sqrt{2}}{2}$．
如图，等边△ABC的边长为2，BD是高，延长BC到点E，使CE=CD，则DE的长为$\sqrt{3}$．
8．a，b，c为常数，且（a-c）2＞a2+c2，则关于x的方程ax2+bx+c=0根的情况是（ ）
| A． | 无实数根 | B． | 有两个相等的实数根 | ||
| C． | 有两个不相等的实数根 | D． | 有一根为0 |