题目内容
20.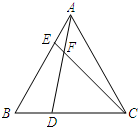 如图,在等边△ABC中,点D,E分别在边BC,AB上,AD与CE交于点F,CE=AD,∠DFC=60度.求证:BD=AE.
如图,在等边△ABC中,点D,E分别在边BC,AB上,AD与CE交于点F,CE=AD,∠DFC=60度.求证:BD=AE.
分析 根据等边三角形的性质和三角形内角和定理求出∠ACE=∠EAF,再根据AAS证出△AEC≌△BDA,即可得出BD=AE.
解答 解:∵∠DFC=60°,
∴∠AFE=60°,
∴∠AEF+∠EAF=120°,
∵△ABC是等边三角形,
∴∠B=60°,∠EAC=60°,
∴∠ACE+∠AEF=120°,
∴∠ACE=∠EAF,
在△AEC和△BDA中,
$\left\{\begin{array}{l}{∠EAC=∠B}\\{∠EAF=∠ACE}\\{CE=AD}\end{array}\right.$,
∴△AEC≌△BDA(AAS),
∴BD=AE.
点评 本题考查了等边三角形的性质和全等三角形的性质与判定;解题的关键是利用三角形内角和定理求出∠ACE=∠EAF.

练习册系列答案
相关题目
8.下列计算不正确的是( )
| A. | (-3)0=-1 | B. | 3.8×10-5=0.000038 | ||
| C. | 20020=20030 | D. | ($\frac{1}{4}$)-2=16 |
5.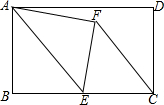 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
 如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )
如图,在矩形ABCD中,AB=8,BC=12,点E是BC的中点,连接AE,将△ABE沿AE折叠,点B落在点F处,连接FC,则tan∠ECF=( )| A. | $\frac{3}{4}$ | B. | $\frac{4}{3}$ | C. | $\frac{3}{5}$ | D. | $\frac{4}{5}$ |
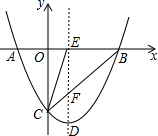 如图,二次函数y=x2+bx+c的图象分别与x轴、y轴相交于A、B、C三点,其对称轴与x轴、线段BC分别交于点E、点F,连接CE,已知点A(-1,0),C(0,-3).
如图,二次函数y=x2+bx+c的图象分别与x轴、y轴相交于A、B、C三点,其对称轴与x轴、线段BC分别交于点E、点F,连接CE,已知点A(-1,0),C(0,-3).