题目内容
6.已知菱形的面积为6$\sqrt{2}$,一条对角线长为2$\sqrt{6}$,求另一条对角线的长及菱形的周长.分析 根据菱形的面积等于两条对角线的积的一半,可求得另一条对角线的长,再根据菱形的对角线垂直且互相平分以及勾股定理可求出菱形的边长,进而可求出其周长.
解答 解:设菱形的另一条对角线长为x,则$\frac{1}{2}$×2$\sqrt{6}$×x=6$\sqrt{2}$,
解得:x=2$\sqrt{3}$,
∵据菱形的对角线垂直且互相平分,
∴及菱形的边长=$\sqrt{6+3}$=3,
∴菱形的周长=12.
点评 本题考查了菱形对角线互相垂直平分的性质,注意菱形各边长相等的性质,勾股定理在直角三角形中的运用,本题中根据勾股定理求菱形边长的值是解题的关键.

练习册系列答案
相关题目
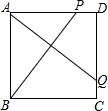 如图,A、B、C、D四家工厂分别坐落在正方形城镇的四个角上,仓库P和Q分别位于AD和DC上,且PD=QC,证明两条直路BP=AQ且BP⊥AQ.
如图,A、B、C、D四家工厂分别坐落在正方形城镇的四个角上,仓库P和Q分别位于AD和DC上,且PD=QC,证明两条直路BP=AQ且BP⊥AQ.