题目内容
19．从边长为2cm的正方形中，剪下一个面积最大的扇形，用其围成一个圆锥体，则这个圆锥体的底面半径是$\frac{1}{2}$cm．分析 正方形中以顶点为圆心、边长为半径的扇形面积最大，根据扇形弧长等于圆锥底面圆周长可求得半径．
解答 解：根据题意，该最大扇形的弧长为$\frac{90•π•2}{180}$=π，
设圆锥的底面半径为r，
则2πr=π，
解得：r=$\frac{1}{2}$，
故答案为：$\frac{1}{2}$．
点评 本题考查了圆锥的计算，正确理解圆锥的底面圆周长是扇形的弧长是解决本题的关键．
练习册系列答案
相关题目
4．五张完全相同的卡片上，分别写上数字-3，-2，-1，2，3，现从中随机抽取一张，抽到写有负数的卡片的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{2}{5}$ | C． | $\frac{3}{5}$ | D． | $\frac{4}{5}$ |
如图，在矩形ABCD中，AB=8，BC=12，点E是BC的中点，连接AE，将△ABE沿AE折叠，点B落在点F处，连接FC，求证：AE∥CF．
8．2的平方根是（ ）
| A． | ±$\sqrt{2}$ | B． | $\sqrt{2}$ | C． | ±1.414 | D． | 4 |
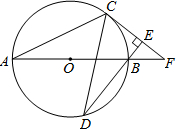如图，AB为⊙O的直径，C，D为⊙O上不同于A，B的两点，过点C作⊙O的切线CF交直线AB于点F，直线DB⊥CF于点E．