题目内容
11.抛物线y=-2x2+3x-1的对称轴是x=$\frac{3}{2}$,与y轴的交点坐标是(0,-1),与x轴的交点坐标是(1,0)和($\frac{1}{2}$,0).分析 利用对称轴公式x=-$\frac{b}{2a}$可以求出对称轴,分别令x=0或y=0可以求出抛物线与y轴或x轴的交点坐标.
解答 解:抛物线y=-2x2+3x-1的对称轴x=-$\frac{b}{2a}$=-$\frac{3}{-2}$=$\frac{3}{2}$.
令x=0,y=-1,所以抛物线与y轴的交点为(0,-1),
令y=0,则-2x2+3x-1=0,解得x=1或$\frac{1}{2}$,所以抛物线与x轴的交点为(1,0),($\frac{1}{2}$,0),
故答案为:x=$\frac{3}{2}$;(0,-1);(1,0)和($\frac{1}{2}$,0).
点评 本题考查抛物线与坐标轴的交点、对称轴等知识,熟练掌握这些基本知识是解决问题的关键,记住对称轴公式x=-$\frac{b}{2a}$,也可以由用配方法求,属于中考常考题型.

练习册系列答案
 应用题作业本系列答案
应用题作业本系列答案
相关题目
20.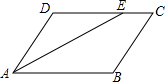 如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为( )
如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为( )
 如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为( )
如图所示,折叠平行四边形的一边AD,使点A落在DC边上的点E处,已知AB=6,BC=4,则EC的长为( )| A. | 1 | B. | 2 | C. | 3 | D. | 1.5 |
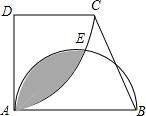 如图,∠D=∠DAB=90°,AD=CD=$\sqrt{3}$,AB=2,以D为圆心,AD为半径作扇形AEC,以AB为直径作半圆,则圆中阴影部分的面积为$\frac{5π}{6}-\sqrt{3}$.
如图,∠D=∠DAB=90°,AD=CD=$\sqrt{3}$,AB=2,以D为圆心,AD为半径作扇形AEC,以AB为直径作半圆,则圆中阴影部分的面积为$\frac{5π}{6}-\sqrt{3}$.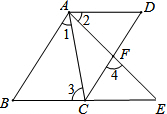 如图,AB∥CD,AD∥BE,∠1=∠2,证明:∠3=∠4.
如图,AB∥CD,AD∥BE,∠1=∠2,证明:∠3=∠4.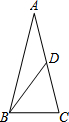 如图,在△ABC中,AB=AC=4,cosC=$\frac{1}{4}$,BD是中线,将△CBD沿直线BD翻折后,点C落在点E,那么AE的长为$\sqrt{6}$.
如图,在△ABC中,AB=AC=4,cosC=$\frac{1}{4}$,BD是中线,将△CBD沿直线BD翻折后,点C落在点E,那么AE的长为$\sqrt{6}$.