题目内容
观察下列等式:12=1,12-22=-3,12-22+32=6,12-22+32-42=-10,…依次规律,则第十个等式的右边等于 .
考点:规律型:数字的变化类
专题:
分析:等式的左边是正整数的平方和或差,根据这一规律得第n个等式左边为12-22+32-42+…(-1)n-1n2.再分n为奇数和偶数讨论,结合分组求和法求和,最后利用字母表示即可.
解答:解:观察下列等式:
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
…
分n为奇数和偶数讨论:
第n个等式左边为12-22+32-42+…(-1)n-1n2.
当n为偶数时,分组求和(12-22)+(32-42)+…+[n-1)2-n2]=-
,
当n为奇数时,第n个等式左边=12-22)+(32-42)+…+[n-1)2-n2]=-
+n2=
.
所以第十个等式的右边等于-
=-55.
故答案为:-55.
12=1
12-22=-3
12-22+32=6
12-22+32-42=-10
…
分n为奇数和偶数讨论:
第n个等式左边为12-22+32-42+…(-1)n-1n2.
当n为偶数时,分组求和(12-22)+(32-42)+…+[n-1)2-n2]=-
| n(n+1) |
| 2 |
当n为奇数时,第n个等式左边=12-22)+(32-42)+…+[n-1)2-n2]=-
| n(n+1) |
| 2 |
| n(n+1) |
| 2 |
所以第十个等式的右边等于-
| 10×(10+1) |
| 2 |
故答案为:-55.
点评:此题考查规律型中的数字变化问题,找等式的规律时,既要分别看左右两边的规律,还要注意看左右两边之间的联系.

练习册系列答案
 寒假大串联黄山书社系列答案
寒假大串联黄山书社系列答案
相关题目
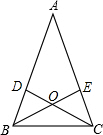 如图,△ABC中,AB=AC,∠A=36°,CD、BE是△ABC的角平分线,CD、BE相交于点O,则图中等腰三角形有( )
如图,△ABC中,AB=AC,∠A=36°,CD、BE是△ABC的角平分线,CD、BE相交于点O,则图中等腰三角形有( )| A、6个 | B、7个 | C、8个 | D、9个 |
已知a=2-
,b=
-2,则a、b的关系是( )
| 3 |
| 3 |
| A、a=b | B、ab=1 |
| C、ab=-1 | D、a+b=0 |
 如图,点D是等腰△ABC的底边AB上的点,若AC=BC且∠ACB=100°,将△ACD绕点C逆时针旋转,使它与△BCD′重合,则∠D′BA=
如图,点D是等腰△ABC的底边AB上的点,若AC=BC且∠ACB=100°,将△ACD绕点C逆时针旋转,使它与△BCD′重合,则∠D′BA= 如图,在△ABC中,D是BC的中点,设
如图,在△ABC中,D是BC的中点,设