题目内容
3.先化简,再求值:($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{x}^{2}-2x+1}$,其中sin30°<x<tan45°,请你取一个合适的数作为x的值代入求值.分析 先算括号内的减法,同时把除法变成乘法,再算乘法,取符合条件的x的值代入,即可求出答案.
解答 解:($\frac{3x+4}{{x}^{2}-1}$-$\frac{2}{x-1}$)÷$\frac{x+2}{{x}^{2}-2x+1}$
=[$\frac{3x+4}{(x+1)(x-1)}$-$\frac{2(x+1)}{(x+1)(x-1)}$]•$\frac{(x-1)^{2}}{x+2}$
=$\frac{3x+4-2x-2}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+2}$
=$\frac{x+2}{(x+1)(x-1)}$•$\frac{(x-1)^{2}}{x+2}$
=$\frac{x-1}{x+1}$,
∵sin30°<x<tan45°,
∴取x=$\frac{3}{4}$,
∴原式=$\frac{\frac{3}{4}-1}{\frac{3}{4}+1}$=-$\frac{1}{7}$.
点评 本题考查了分式的混合运算和求值,特殊角的三角函数值的应用,能综合运用分式的运算法则进行化简是解此题的关键,综合比较强,有一定的难度,注意运算顺序.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.|-$\frac{1}{2015}$|的相反数是( )
| A. | 2015 | B. | -2015 | C. | $\frac{1}{2015}$ | D. | -$\frac{1}{2015}$ |
12.可以来证明命题“若a2<0.04,则a<0.2”是假命题的反例( )
| A. | 可以是a=-0.2,不可以是a=-2 | |
| B. | 可以是a=-2,不可以是a=-0.2 | |
| C. | 可以是a=-0.2,也可以是a=-2 | |
| D. | 既不可以是a=-0.2,也不可以是a=-2 |
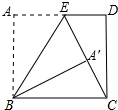 如图,矩形ABCD中,AB=15cm,点E在AD上,AE=9cm,连接EC,将矩形ABCD沿BE翻折,点A恰好落在EC上的点A′处,则BC=17cm.
如图,矩形ABCD中,AB=15cm,点E在AD上,AE=9cm,连接EC,将矩形ABCD沿BE翻折,点A恰好落在EC上的点A′处,则BC=17cm. 如图所示,若四条直线两两相交于不同点,则图中有12对对顶角,有48对同位角,有24对内错角,有24对同旁内角.
如图所示,若四条直线两两相交于不同点,则图中有12对对顶角,有48对同位角,有24对内错角,有24对同旁内角.