题目内容
12.化简求值:$\frac{{x}^{2}-1}{{x}^{2}-x}$÷(1+$\frac{{x}^{2}+1}{2x}$),其中x=$\sqrt{3}$-1.分析 先根据分式混合运算的法则把原式进行化简,再把x的值代入进行计算即可.
解答 解:原式=$\frac{x+1}{x}$÷$\frac{(x+1)^{2}}{2x}$
=$\frac{x+1}{x}$•$\frac{2x}{(x+1)^{2}}$
=$\frac{2}{x+1}$,
当x=$\sqrt{3}$-1时,原式=$\frac{2}{\sqrt{3}-1+1}$=$\frac{2\sqrt{3}}{3}$.
点评 本题考查的是分式的化简求值,熟知分式混合运算的法则是解答此题的关键.

练习册系列答案
 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案
相关题目
8.下列一次函数中,y随x增大而减小的是( )
| A. | y=2x | B. | y=3x-2 | C. | y=-5x+2 | D. | y=2x-2 |
7.下列计算正确的是( )
| A. | (a2)3=a6 | B. | a3•a2=a6 | C. | 2a+3a2=5a3 | D. | $3{a^3}÷2a=\frac{3}{2}{a^3}$ |
2.如果分式$\frac{x-3}{2x+1}$有意义,则x的取值范围是( )
| A. | x≠3 | B. | x$≠-\frac{1}{2}$ | C. | x=-$\frac{1}{2}$ | D. | x=3 |
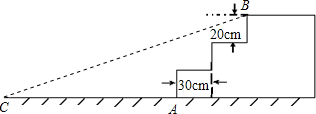 奥运会期间,某公园入口处原有三级台阶,为方便残疾人士,拟将台阶改为斜坡,每级台阶高为20cm,深为30cm.设台阶的起点为A,斜坡的起始点为C,现将斜坡的坡角∠BCA设计为12°,求AC的长度.(参考数据:tan12°=$\frac{3}{14}$)
奥运会期间,某公园入口处原有三级台阶,为方便残疾人士,拟将台阶改为斜坡,每级台阶高为20cm,深为30cm.设台阶的起点为A,斜坡的起始点为C,现将斜坡的坡角∠BCA设计为12°,求AC的长度.(参考数据:tan12°=$\frac{3}{14}$)