题目内容
6.计算:(1)$\frac{cos30°-sin45°}{sin60°-cos45°}$;
(2)sin230°+2sin60°+tan45°-tan60°+cos230°;
(3)$\sqrt{1-2tan60°+ta{n}^{2}60°}$-tan60°.
分析 (1)直接把各特殊角的三角函数值代入进行计算即可;
(2)根据sin230°+cos230°=1,再把各特殊角的三角函数值代入进行计算即可;
(3)把被开方数化为完全平方的性质,再把各特殊角的三角函数值代入进行计算即可.
解答 解:(1)原式=$\frac{\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}}{\frac{\sqrt{3}}{2}-\frac{\sqrt{2}}{2}}$=1;
(2)原式=1+2sin60°+tan45°-tan60°
=1+2×$\frac{\sqrt{3}}{2}$+1-$\sqrt{3}$
=2;
(3)原式=$\sqrt{(1-tan60°)^{2}}$-tan60°
=$\sqrt{{(1-\sqrt{3})}^{2}}$-$\sqrt{3}$
=$\sqrt{3}$-1-$\sqrt{3}$
=-1.
点评 本题考查的是特殊角的三角函数值,熟记各特殊角的三角函数值是解答此题的关键.

练习册系列答案
相关题目
 如图:在△ABC中,∠C=45°,BC=2$\sqrt{2}$,AC=6,求tanA和△ABC的面积.
如图:在△ABC中,∠C=45°,BC=2$\sqrt{2}$,AC=6,求tanA和△ABC的面积.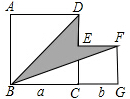 如图,两个正方形的边长分别为acm,bcm(a>b),若a+b=5cm,ab=3cm,求图中阴影部分的面积.
如图,两个正方形的边长分别为acm,bcm(a>b),若a+b=5cm,ab=3cm,求图中阴影部分的面积.
 将一张矩形的纸对折再折,然后沿着左图中的虚线剪下打开,你发现这是一个等腰梯形.
将一张矩形的纸对折再折,然后沿着左图中的虚线剪下打开,你发现这是一个等腰梯形.