题目内容
4.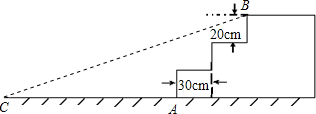 奥运会期间,某公园入口处原有三级台阶,为方便残疾人士,拟将台阶改为斜坡,每级台阶高为20cm,深为30cm.设台阶的起点为A,斜坡的起始点为C,现将斜坡的坡角∠BCA设计为12°,求AC的长度.(参考数据:tan12°=$\frac{3}{14}$)
奥运会期间,某公园入口处原有三级台阶,为方便残疾人士,拟将台阶改为斜坡,每级台阶高为20cm,深为30cm.设台阶的起点为A,斜坡的起始点为C,现将斜坡的坡角∠BCA设计为12°,求AC的长度.(参考数据:tan12°=$\frac{3}{14}$)
分析 过B点作BD⊥CD,可得Rt△CBD,根据每级台阶高为20cm,可得BD=60cm,然后根据∠BCA=12°,利用三角函数的知识解直角三角形求出CD的长度,继而可求出AC的长度.
解答 解:过B点作BD⊥CD,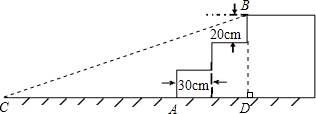
则△CBD为直角三角形,
∵tan∠BCA=tan12°=$\frac{BD}{CD}$=$\frac{3}{14}$,
∴$\frac{60}{CD}$=$\frac{3}{14}$,
∴CD=280,
∴AC=CD-60=220(cm).
即AC的长度为220cm.
点评 本题考查了解直角三角线的应用,解答本题的关键是根据坡度构造直角三角形,利用三角函数的知识求解直角三角形.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
16.有15位同学参加学校组织的才艺表演比赛,已知他们所得的分数互不相同,共设8个获奖名额,某同学知道自己的比赛分数后,要判断自己能否获奖,在下列15位同学成绩的统计量中只需知道一个量,它是( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
13.如果把分数$\frac{ab}{a+b}$(a和b都不为0)中的a,b都扩大2倍,那么分式的值一定( )
| A. | 不变 | B. | 是原来的2倍 | C. | 是原来的3倍 | D. | 是原来的4倍 |
 一个粮仓如图,请您细心算出这个粮仓的容积是1.7π立方米.
一个粮仓如图,请您细心算出这个粮仓的容积是1.7π立方米.