题目内容
4．方程x2-2x+m=0有两个不相等的实数根，m值可能为（ ）| A． | 0 | B． | 1 | C． | 2 | D． | 3 |
分析 先根据方程有两个不相等的实数根得出m的不等式，求出m的取值范围即可．
解答 解：∵方程x2-2x+m=0有两个不相等的实数根，
∴△=（-2）2-4m＞0，解得m＜1，
∴m的值可能为0．
故选A．
点评 本题考查的是根的判别式，熟知一元二次方程的根与判别式△=b2-4ac的关系是解答此题的关键．
练习册系列答案
相关题目
2．
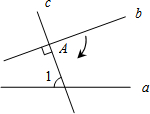如图，直线a与直线b被直线c所截，b⊥c，垂足为点A，∠1=70°．若使直线b与直线a平行，则可将直线b绕着点A顺时针旋转（ ）
如图，直线a与直线b被直线c所截，b⊥c，垂足为点A，∠1=70°．若使直线b与直线a平行，则可将直线b绕着点A顺时针旋转（ ）| A． | 70° | B． | 50° | C． | 30° | D． | 20° |
16．
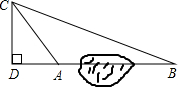如图，在一次课外活动中，同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离，已知CD⊥BD，现测得AC=30m，BC=70m，CD=15$\sqrt{3}$m，请计算A、B两个凉亭之间的距离．
如图，在一次课外活动中，同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离，已知CD⊥BD，现测得AC=30m，BC=70m，CD=15$\sqrt{3}$m，请计算A、B两个凉亭之间的距离．
14．甲、乙两人从同一起点沿着同一条公路骑自行车比赛，两人同向而行，如果甲让乙先骑6m，则甲骑了6s就可追上乙；如果甲让乙先骑3s，则甲骑了4s还离乙20m；若设甲的平均速度为x m/s，乙的平均速度为y m/s，则根据题意列出方程组为（ ）
| A． | $\left\{\begin{array}{l}{6y=6x+6}\\{4x=7y+20}\end{array}\right.$ | B． | $\left\{\begin{array}{l}{6x-6y=6}\\{4x=7y-20}\end{array}\right.$ | ||
| C． | $\left\{\begin{array}{l}{6x+6=6y}\\{4x-4y=3y-20}\end{array}\right.$ | D． | $\left\{\begin{array}{l}{6x-6=6y}\\{4x-4y=3y+20}\end{array}\right.$ |