题目内容
16.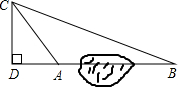 如图,在一次课外活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离,已知CD⊥BD,现测得AC=30m,BC=70m,CD=15$\sqrt{3}$m,请计算A、B两个凉亭之间的距离.
如图,在一次课外活动中,同学们要测量某公园人工湖两侧A、B两个凉亭之间的距离,已知CD⊥BD,现测得AC=30m,BC=70m,CD=15$\sqrt{3}$m,请计算A、B两个凉亭之间的距离.
分析 先在Rt△CDA中求得AD、CD的长,再利用勾股定理求得BD的长,AB=BD-AD.
解答 解:在Rt△CDA中,AC=30m,∠CAD=180°-∠CAB=180°-120°=60°.
∴CD=AC•sin∠CAD=30•sin60°=15$\sqrt{3}$m.
AD=AC•cos∠CAD=30•cos60°=15m.
在Rt△CDB中,∵BC=70,BD2=BC2-CD2,
∴BD=$\sqrt{7{0}^{2}-(15\sqrt{3})^{2}}$=65m.
∴AB=BD-AD=65-15=50m.
答:A,B两个凉亭之间的距离为50m.
点评 考查了勾股定理的应用,解一般三角形的问题一般可以转化为解直角三角形的问题,解决的方法就是作高线.

练习册系列答案
相关题目
4.方程x2-2x+m=0有两个不相等的实数根,m值可能为( )
| A. | 0 | B. | 1 | C. | 2 | D. | 3 |
6.已知三角形两边的长分别是3和9,则此三角形第三边的长可能是( )
| A. | 5 | B. | 6 | C. | 11 | D. | 13 |
 已知二次函数的图象与x轴的交点坐标为(3,0)和(-1,0),且经过点(1,-4),
已知二次函数的图象与x轴的交点坐标为(3,0)和(-1,0),且经过点(1,-4),