题目内容
12.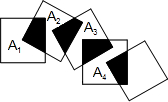 将2015个边长都为1cm的正方形按如图所示摆放,点A1,A2,A3…分别是正方形对角线的交点,则这个2015个正方形重叠部分的面积和为$\frac{1007}{2}$cm2.
将2015个边长都为1cm的正方形按如图所示摆放,点A1,A2,A3…分别是正方形对角线的交点,则这个2015个正方形重叠部分的面积和为$\frac{1007}{2}$cm2.
分析 根据题意可得,阴影部分的面积是正方形的面积的$\frac{1}{4}$,已知两个正方形可得到一个阴影部分,则2015个这样的正方形重叠部分即为2015-1阴影部分的和,问题得解.
解答 解:由题意可得阴影部分面积等于正方形面积的$\frac{1}{4}$,即是$\frac{1}{4}$cm2.
5个这样的正方形重叠部分(阴影部分)的面积和为$\frac{1}{4}$×4cm2,
n个这样的正方形重叠部分(阴影部分)的面积和为$\frac{1}{4}$×(n-1)=$\frac{n-1}{4}$cm2.
所以这个2015个正方形重叠部分的面积和=$\frac{1}{4}$×(2005-1)=$\frac{1007}{2}$cm2,
故答案为:$\frac{1007}{2}$.
点评 考查了正方形的性质,解决本题的关键是得到n个这样的正方形重叠部分(阴影部分)的面积和的计算方法,难点是求得一个阴影部分的面积.

练习册系列答案
相关题目
20.把多项式5x3-5x进行因式分解正确的结果是( )
| A. | 5x3-5x=5(x3-x) | B. | 5x3-5x=5x(x2-1) | ||
| C. | 5x3-5x=5x(x+1)(x-1) | D. | 5x3-5x=5x2(1+$\frac{1}{x}$)(x-1) |
4.下列正多边形的地砖中,不能铺满地面的正多边形是( )
| A. | 正三角形 | B. | 正方形 | C. | 正五边形 | D. | 正六边形 |
 如图,在平面直角坐标系中,己知点A(-1,3)和点B(2,2),若四边ABCD是正方形,则点C的坐标为(2,-1)或(3,5).
如图,在平面直角坐标系中,己知点A(-1,3)和点B(2,2),若四边ABCD是正方形,则点C的坐标为(2,-1)或(3,5).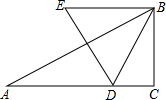 如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.
如图,己知△ABC中,∠C=90°,∠A=30°,AC=$\sqrt{3}$.动点D在边AC上,以BD为边作等边△BDE(点E、A在BD的同侧).在点D从点A移动至点C的过程中,点E移动的路线长为$\sqrt{3}$.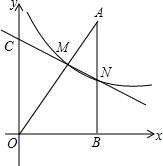 如图,在平面直角坐标系中,A点的坐标是(3,4),AB⊥x轴于点B,反比例函数y=$\frac{k}{x}$的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM.
如图,在平面直角坐标系中,A点的坐标是(3,4),AB⊥x轴于点B,反比例函数y=$\frac{k}{x}$的图象中的一支经过线段OA上一点M,交AB于点N,已知OM=2AM.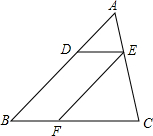 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.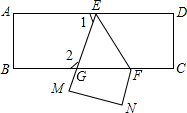 把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,则∠1=70°.
把一张长方形纸片ABCD沿EF折叠后ED与BC的交点为G,D、C分别在M、N的位置上,若∠EFG=55°,则∠1=70°.