题目内容
1.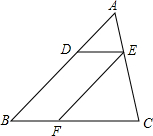 如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.
如图,已知在△ABC中,点D、E、F分别是边AB、AC、BC上的点,DE∥BC,EF∥AB,且AD:AB=3:8,那么S△ADE:S△EFC=9:25.
分析 根据平行线分线段成比例定理求出AE:AC=AD:AB=3:8,求出AE:CE=3:5,根据平行线的性质得出∠A=∠EFC,∠AED=∠C,根据相似三角形的判定得出△ADE∽△EFC,根据相似三角形的性质得出即可.
解答 解:∵DE∥BC,AD:AB=3:8,
∴AE:AC=AD:AB=3:8,
∴AE:CE=3:5,
∵DE∥BC,EF∥AB,
∴∠A=∠EFC,∠AED=∠C,
∴△ADE∽△EFC,
∴$\frac{{S}_{△ADE}}{{S}_{△EFC}}$=($\frac{AE}{CE}$)2=($\frac{3}{5}$)2=$\frac{9}{25}$,
故答案为:9:25.
点评 本题考查了相似三角形的性质和判定,平行线分线段成比例定理的应用,能灵活运用定理进行推理是解此题的关键,注意:相似三角形的面积之比等于相似比的平方.

练习册系列答案
相关题目
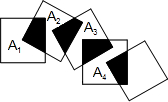 将2015个边长都为1cm的正方形按如图所示摆放,点A1,A2,A3…分别是正方形对角线的交点,则这个2015个正方形重叠部分的面积和为$\frac{1007}{2}$cm2.
将2015个边长都为1cm的正方形按如图所示摆放,点A1,A2,A3…分别是正方形对角线的交点,则这个2015个正方形重叠部分的面积和为$\frac{1007}{2}$cm2.
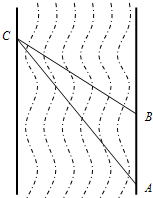 小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.
小明同学需测量一条河流的宽度(河岸两边互相平行).如图,小明同学在河岸一侧选取两个观测点A、B,在河对岸选取观测点C,测得AB=31m,∠CAB=37°,∠CBA=120°.请你根据以上数据,帮助小明计算出这条河的宽度.