题目内容
2. 如图,在平面直角坐标系中,己知点A(-1,3)和点B(2,2),若四边ABCD是正方形,则点C的坐标为(2,-1)或(3,5).
如图,在平面直角坐标系中,己知点A(-1,3)和点B(2,2),若四边ABCD是正方形,则点C的坐标为(2,-1)或(3,5).
分析 过A、C两点作y轴的平行线与过点B平行于x轴的直线交于点F、E两点,过点B作x轴的垂线交过点C平行于x轴的直线于点M.只要证明△ABF≌△CBM≌△C′BE即可解决问题.
解答 解: 过A、C两点作y轴的平行线与过点B平行于x轴的直线交于点F、E两点,
过A、C两点作y轴的平行线与过点B平行于x轴的直线交于点F、E两点,
过点B作x轴的垂线交过点C平行于x轴的直线于点M.
∵四边形ABCD,四边形ABC′D′是正方形,
∴AB=CB,∠ABC=∠FBM,
∴∠ABF=∠CBM,
在△ABF和△CBM中,
$\left\{\begin{array}{l}{∠AFB=∠CMB=90°}\\{∠ABF=∠CBM}\\{AB=BC}\end{array}\right.$
∴△ABF≌△CBM,
∴CM=AF=1,BF=BM=3,
∴点C坐标(1,-1),同理可得点C′坐标(3,5).
故答案为(1,-1)和(3,5).
点评 本题考查正方形性质、坐标与图形的性质、全等三角形的判定和性质等知识,解题的关键是添加辅助线构造全等三角形,属于中考常考题型.

练习册系列答案
 精英口算卡系列答案
精英口算卡系列答案 应用题点拨系列答案
应用题点拨系列答案 状元及第系列答案
状元及第系列答案 同步奥数系列答案
同步奥数系列答案
相关题目
2. 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
 如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )
如图,点A的坐标为(0,1),点B是x轴正半轴上的一动点,以AB为边作等腰直角△ABC,使∠BAC=90°,设点B的横坐标为x,点C的纵坐标为y,能表示y与x的函数关系的图象大致是( )| A. | 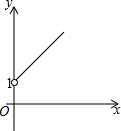 | B. | 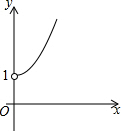 | C. | 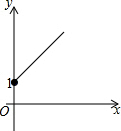 | D. | 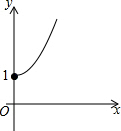 |
7.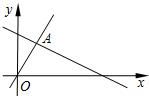 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则m+a的值为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则m+a的值为( )
 如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则m+a的值为( )
如图,函数y=2x和y=ax+4的图象相交于点A(m,3),则m+a的值为( )| A. | -1 | B. | $\frac{5}{6}$ | C. | 1 | D. | $\frac{13}{6}$ |
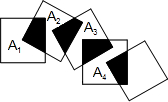 将2015个边长都为1cm的正方形按如图所示摆放,点A1,A2,A3…分别是正方形对角线的交点,则这个2015个正方形重叠部分的面积和为$\frac{1007}{2}$cm2.
将2015个边长都为1cm的正方形按如图所示摆放,点A1,A2,A3…分别是正方形对角线的交点,则这个2015个正方形重叠部分的面积和为$\frac{1007}{2}$cm2.