题目内容
 墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.5m,小明向墙壁走1m到B处发现影子刚好落在A点,则灯泡与地面的距离CD=
墙壁D处有一盏灯(如图),小明站在A处测得他的影长与身长相等都为1.5m,小明向墙壁走1m到B处发现影子刚好落在A点,则灯泡与地面的距离CD=考点:相似三角形的应用,中心投影
专题:
分析:利用已知条件易证△EAF∽△ECD,△ABG∽△ACD,设BC=xm,CD=ym,则CE=(x+2.5)m,AC=(x+1)m,利用相似三角形的性质:对应边的比值相等,列出方程组,通过解方程组求出灯泡与地面的距离即可.
解答:解:如图:
根据题意得:BG=AF=AE=1.5m,AB=1m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.5)m,AC=(x+1)m,
=
,
=
,
解得:y=7.5,
所以CD=7.5m,
故答案为:7.5m.
根据题意得:BG=AF=AE=1.5m,AB=1m,
∵BG∥AF∥CD,
∴△EAF∽△ECD,△ABG∽△ACD,
∴AE:EC=AF:CD,AB:AC=BG:CD,
设BC=xm,CD=ym,则CE=(x+2.5)m,AC=(x+1)m,
| 1 |
| x+2.5 |
| 1.6 |
| y |
| 1 |
| x+1 |
| 1.5 |
| y |
解得:y=7.5,
所以CD=7.5m,
故答案为:7.5m.
点评:此题主要考查了相似三角形的应用,把实际问题抽象到相似三角形中,利用相似三角形的相似比,列出方程组是解题关键.

练习册系列答案
相关题目
下列各式正确的是( )
A、
| ||||||
B、3
| ||||||
C、3
| ||||||
D、
|
 如图,学校位于高速路AB的一侧(AB成一直线),点A、点B为高速路上距学校直线距离最近的2个隧道出入口,点C、点D为学校的两幢教学楼.经测量,∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,D到高速路的最短直线距离DE=400m.
如图,学校位于高速路AB的一侧(AB成一直线),点A、点B为高速路上距学校直线距离最近的2个隧道出入口,点C、点D为学校的两幢教学楼.经测量,∠ACB=90°,∠ADB>90°,AC=600m,AB=1000m,D到高速路的最短直线距离DE=400m.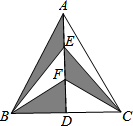 如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若△ABC的面积为10cm2,则图中阴影部分的面积是
如图,在△ABC中,AB=AC,AD是BC边上的高,点E,F是AD上的任意两点,若△ABC的面积为10cm2,则图中阴影部分的面积是 四边形ABCD是正方形,圆心角等于90°,OE=OF=10,问:正方形边长多少?
四边形ABCD是正方形,圆心角等于90°,OE=OF=10,问:正方形边长多少?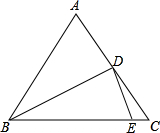 如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD交BC于点E,求证:CD=
如图,在△ABC中,AB=AC,BD平分∠ABC,DE⊥BD交BC于点E,求证:CD=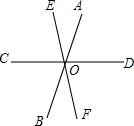 如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF.
如图,直线AB,CD,EF相交于点O,∠AOE:∠AOD=1:3,∠COB:∠DOF=3:4,求证,CD⊥EF. 如图,在B港有“远望1号”和“远望2号”两艘轮船同时出发,若“远望1号”轮船沿北偏东60°方向每小时行驶8n mile,“远望2号”轮船沿南偏东30°方向每小时行驶15n mile,两小时后,两艘轮船分别到达M岛和N岛,求M岛和N岛之间的距离.
如图,在B港有“远望1号”和“远望2号”两艘轮船同时出发,若“远望1号”轮船沿北偏东60°方向每小时行驶8n mile,“远望2号”轮船沿南偏东30°方向每小时行驶15n mile,两小时后,两艘轮船分别到达M岛和N岛,求M岛和N岛之间的距离.