Question

11．已知⊙O₁与⊙O₂的半径分别为3和5，O₁O₂=10．则两圆的两条内公切线与一条外公切线所围成的三角形面积为$\frac{45}{4}$．

Answer 1

分析 作辅助线，根据切线性质得出O₁C⊥CD，O₂D⊥CD、O₁E⊥FM，O₂F⊥FM，则O₁E∥O₂F和PH∥O₂D，
根据平行线分线段成比例定理列比例式求出PG、PH的长，再根据内公切线公式和外公切线公式求出AB和CD的长，从而得出ND、MC的长，根据面积公式代入计算求面积即可．

解答 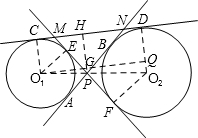解：设外公切线的两个切点分别为C、D，内公切线的四个切点分别为A、E、B、F，连接O₁C、O₂D、O₁E、O₂F，则O₁C⊥CD，O₂D⊥CD、O₁E⊥FM，O₂F⊥FM，
过P作PH⊥CD于H，过O₁作O₁Q⊥O₂D于Q，两垂线交于点G，连接O₁O₂，则O₁、O₂经过点P；
∵O₁E⊥FM，O₂F⊥FM，
∴O₁E∥O₂F，
∴$\frac{{O}_{1}P}{{O}_{2}P}$=$\frac{{O}_{1}E}{{O}_{2}F}$=$\frac{3}{5}$，
∵PH⊥CD，O₂D⊥CD，
∴PH∥O₂D，
∴$\frac{PG}{{O}_{2}Q}$=$\frac{{O}_{1}P}{{O}_{1}{O}_{2}}$=$\frac{3}{8}$，
∴$\frac{PG}{5-3}=\frac{3}{8}$，
∴PG=$\frac{3}{4}$，
∴PH=3+$\frac{3}{4}$=$\frac{15}{4}$，
∵AN=CN，
即AB+BN=CN，
∵CD=CN+DN，
∴CD=AB+BN+ND，
∵ND=BN，
∴BN=ND=$\frac{CD-AB}{2}$，
∵CD=O₁Q=$\sqrt{1{0}^{2}-（5-3）^{2}}$=4$\sqrt{6}$，
AB=$\sqrt{1{0}^{2}-（5+3）^{2}}$=6，
∴ND=$\frac{4\sqrt{6}-6}{2}$=2$\sqrt{6}$-3，
同理得：CM=2$\sqrt{6}$-3，
∴MN=CD-CM-ND=4$\sqrt{6}$-2（2$\sqrt{6}$-3）=6，
∴S_△PMN=$\frac{1}{2}$MN•PH=$\frac{1}{2}$×6×$\frac{15}{4}$=$\frac{45}{4}$，
故答案为：$\frac{45}{4}$．

点评 本题考查了相离两圆的外公切线和内公切线的性质，首先要确定其所成的三角形，根据面积公式求两边MN和FH的长，因此要熟练掌握圆的切线垂直于经过切点的半径，同时运用了平行线分线段成比例定理和勾股定理求边的长，代入面积公式即可得出结论．