Question

2．如图，在平面直角坐标系中，直角三角形的直角顶点放在点A（2，2）处，两直角边分别交x轴、y轴于B、C两点．
（1）若B在x轴正半轴，C在y轴正半轴，求OB+OC的值；
（2）若B在x轴正半轴，C在y轴负半轴，求OB-OC．

Answer 1

分析 （1）如图1，过A作AM⊥x轴于M，AN⊥y轴于N，则∠ANC=∠AMB=90°，∠NAM=90°，进而推出△ANC≌△AMB，即可得出答案；
（2）如图2，过A作AM⊥x轴于M，AN⊥y轴于N，求出△ANC≌△AMB，根据全等得出CN=BM，求出OB-OC=OM+ON，代入求出即可．

解答 解：（1）如图1，过A作AM⊥x轴于M，AN⊥y轴于N，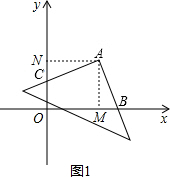

则∠ANC=∠AMB=90°，∠NAM=90°，
∵∠BAC=90°，
∴∠NAC=∠BAN=90°-∠CAM，
∵A（2，2），
∴AM=AN=2，
在△ANC和△AMB中
$\left\{\begin{array}{l}{∠ANC=∠AMB}\\{AN=AM}\\{∠NAC=∠MAB}\end{array}\right.$
∴△ANC≌△AMB，
∴NC=MB，
∴OB+OC=OM+ON=2+2=4；

（2）如图2，过A作AM⊥x轴于M，AN⊥y轴于N，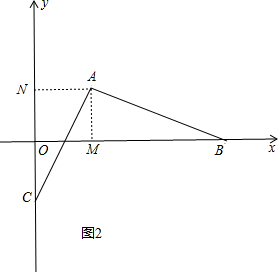
则∠ANC=∠AMB=90°，∠NAM=90°，
∵∠CAB=90°，
∴∠NAC=∠MAB=90°-∠CAM，
∵A（2，2），
∴AM=AN=2，
在△ANC和△AMB中，
$\left\{\begin{array}{l}{∠ANC=∠AMB}\\{AN=AM}\\{∠CAN=∠BAM}\end{array}\right.$，
∴△CAN≌△BAM（ASA），
∴AC=AB，CN=BM，
∴OB-OC=（OM+BM）-（CN-ON）=OM+ON=2+2=4．

点评 本题考查了坐标与图形性质，全等三角形的性质和判定的应用，能正确作出辅助线并求出△CAN≌△BAM是解此题的关键．