题目内容
17.一杯饮料,第一次倒去一半,第二次倒去剩下的一半…如此倒下去,第n次后剩下饮料是原来的几分之几?$\frac{1}{{2}^{n}}$.分析 设这杯饮料为1,根据题意得第一次后剩下饮料是原来的1-$\frac{1}{2}$=$\frac{1}{2}$,第二次后剩下饮料是原来的1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)=(1-$\frac{1}{2}$)2=$\frac{1}{4}$,第三次后剩下饮料是原来的(1-$\frac{1}{2}$)$\frac{1}{2}$(1-$\frac{1}{2}$)-$\frac{1}{2}$[1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)]=(1-$\frac{1}{2}$)3=$\frac{1}{8}$,由此发现规律,写出第,四次和第n次的结果.
解答 解:设这杯饮料为1,根据题意得
第一次后剩下饮料是原来的:1-$\frac{1}{2}$=$\frac{1}{2}$,
第二次后剩下饮料是原来的:1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)=(1-$\frac{1}{2}$)2=$\frac{1}{4}$,
第三次后剩下饮料是原来的:(1-$\frac{1}{2}$)$\frac{1}{2}$(1-$\frac{1}{2}$)-$\frac{1}{2}$[1-$\frac{1}{2}$-$\frac{1}{2}$(1-$\frac{1}{2}$)]=(1-$\frac{1}{2}$)3=$\frac{1}{8}$,
∴第n次后剩下饮料是原来的:(1-$\frac{1}{2}$)n=$\frac{1}{{2}^{n}}$,
故答案为:$\frac{1}{{2}^{n}}$.
点评 本题主要考查数字的变化规律,根据题意分别计算出第一、二、三次剩余的饮料是解题的关键.

 学而优衔接教材南京大学出版社系列答案
学而优衔接教材南京大学出版社系列答案 小学课堂作业系列答案
小学课堂作业系列答案 金博士一点全通系列答案
金博士一点全通系列答案 如图是用相同的正方形砖铺成的地面,一宝物藏在其中某一块砖的下面,则宝物在白色区域的概率是( )
如图是用相同的正方形砖铺成的地面,一宝物藏在其中某一块砖的下面,则宝物在白色区域的概率是( )| A. | $\frac{2}{5}$ | B. | $\frac{3}{5}$ | C. | $\frac{7}{15}$ | D. | $\frac{8}{15}$ |
| A. | 5 | B. | 6 | C. | 9 | D. | 11 |
| A. | (3,-2) | B. | (2,3) | C. | (2,-3) | D. | (-3,-3) |
| A. | 2006 | B. | 2014 | C. | 2015 | D. | 2016 |
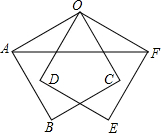 如图,边长为2的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF,连接AF,则AF的长为2$\sqrt{3}$.
如图,边长为2的正方形OABC绕着点O逆时针旋转30°得到正方形ODEF,连接AF,则AF的长为2$\sqrt{3}$.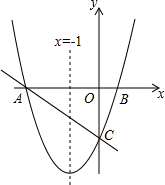 如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中点A的坐标为(-3,0),点C为抛物线与y轴的交点.
如图,对称轴为直线x=-1的抛物线y=x2+bx+c与x轴相交于A,B两点,其中点A的坐标为(-3,0),点C为抛物线与y轴的交点.