题目内容
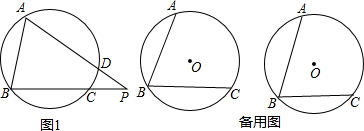
7.已知,锐角∠ABC是⊙O的圆周角,且AB>BC,点D是圆上任意一点(不与A、B、C重合),连接AD并延长交BC所在的直线于点P.(1)如图1,若点D在$\widehat{AC}$上,且∠ABC=80°,求∠CDP的度数;
(2)探索∠CDP与∠ABC的关系;
(3)若$\widehat{AD}=\widehat{BC}$,探索CD与AB的关系(直接写出结论).
分析 (1)因为∠ABC和∠ADC 所对的弧的和是周角,根据圆周角定理得出∠ABC+∠ADC=180°,根据平角的定义得出∠ADC+∠CDP=180°,即可求得∠CDP=∠ABC=80°;
(2)因为∠ABC和∠ADC 所对的弧的和是周角,根据圆周角定理得出∠ABC+∠ADC=180°,根据平角的定义得出∠ADC+∠CDP=180°,即可求得∠CDP=∠ABC;
(3)根据圆心角、弧、弦的关系得出∠1=∠2,然后根据平行线的判定即可证得CD∥AB.
解答  解:(1)∵四边形A、B、C、D四点共圆,
解:(1)∵四边形A、B、C、D四点共圆,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠CDP=180°,
∴∠CDP=∠ABC=80°;
(2)∠CDP=∠ABC,
如图1,∵四边形A、B、C、D四点共圆,
∴∠ABC+∠ADC=180°,
∵∠ADC+∠CDP=180°,
∴∠CDP=∠ABC.
(3)如图2,连接BD,
∵$\widehat{AD}$=$\widehat{BC}$,
∴∠1=∠2,
∴CD∥AB.
点评 本题考查了圆周角定理的应用,圆心角、弧、弦的关系以及平行线的判定,熟练掌握性质定理是解题的关键.

练习册系列答案
相关题目
19.有五个编号分别是Ⅰ、Ⅱ、Ⅲ、Ⅳ和Ⅴ的长方形,大小如表:
(1)通过计算,说明这五个长方形的周长相等;
(2)通过计算,说明长方形Ⅳ、Ⅴ的面积不可能最大.
| 长方形 | Ⅰ | Ⅱ | Ⅲ | Ⅳ | Ⅴ |
| 长度 | 5 | 4 | 3 | 2 | 1 |
| 宽度 | x | x+1 | x+2 | x+3 | x+4 |
(2)通过计算,说明长方形Ⅳ、Ⅴ的面积不可能最大.
16.下列运算中,正确的是( )
| A. | $\sqrt{9}$=±3 | B. | $\root{3}{-8}$=2 | C. | $\sqrt{(-2)^{2}}$=-2 | D. | $\sqrt{18}$-$\sqrt{8}$=$\sqrt{2}$ |
 小明平时爱动脑筋,深受老师喜爱,今天是小明的生日,老师想考小明,特地准备了一个三角形大蛋糕作为礼物,让小明只切三刀,把大蛋糕分成六等份,小明刚学完有关三角形中线的知识,动了一下脑筋,就把问题解决了,你知道小明如何解决的吗?
小明平时爱动脑筋,深受老师喜爱,今天是小明的生日,老师想考小明,特地准备了一个三角形大蛋糕作为礼物,让小明只切三刀,把大蛋糕分成六等份,小明刚学完有关三角形中线的知识,动了一下脑筋,就把问题解决了,你知道小明如何解决的吗?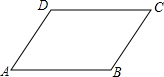 已知?ABCD(如图),将它沿AB方向平移,平移的距离为$\frac{1}{2}$AB.
已知?ABCD(如图),将它沿AB方向平移,平移的距离为$\frac{1}{2}$AB.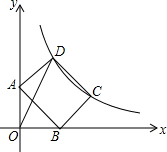 如图所示,矩形ABCD的顶点C、D在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,顶点A在y轴上,顶点B在x轴上,连接OD,若∠ODC=60°,则$\frac{AB}{AD}$=$\sqrt{3}+1$.
如图所示,矩形ABCD的顶点C、D在反比例函数y=$\frac{k}{x}$(k>0,x>0)的图象上,顶点A在y轴上,顶点B在x轴上,连接OD,若∠ODC=60°,则$\frac{AB}{AD}$=$\sqrt{3}+1$.