题目内容
如图，已知∠1=∠2，∠AED=∠C，求证：△ABC∽△ADE．
【考点】相似三角形的判定．
【专题】证明题．
【分析】已经有一角相等，只需再证一角相等即可；由等式的性质得出∠DAE=∠BAC，即可得出结论．
【解答】证明：∵∠1=∠2，
∴∠1+∠BAE=∠2+∠BAE，
即∠DAE=∠BAC，
∵∠AED=∠C，
∴△ABC∽△ADE．
【点评】本题考查了相似三角形的判定方法；熟记两角相等的两个三角形相似是解决问题的关键．
练习册系列答案
小学教材完全解读系列答案
相关题目
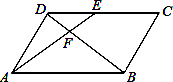
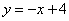，当x=1时，y=3；当x=3时，y=1，即当
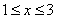时，有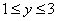
，所以说函数
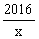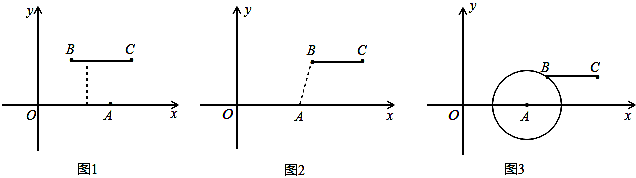
是闭区间[1,2016]上的“闭函数”吗？请判断并说明理由；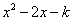
是闭区间[1,2]上的“闭函数”，求k的值；
A．1 B．2