题目内容
设a,b是任意两个不等实数,我们规定:满足不等式a≤x≤b的实数x的所有取值的全体叫做闭区间,表示为[a,b].对于一个函数,如果它的自变量x与函数值y满足:当m≤x≤n时,有m≤y≤n,我们就称此函数是闭区间[m.n]上的“闭函数”.如函数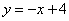 ,当x=1时,y=3;当x=3时,y=1,即当
,当x=1时,y=3;当x=3时,y=1,即当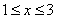 时,有
时,有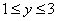 ,所以说函数
,所以说函数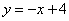 是闭区间[1,3]上的“闭函数”.
是闭区间[1,3]上的“闭函数”.
(1)反比例函数y=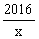 是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;
是闭区间[1,2016]上的“闭函数”吗?请判断并说明理由;
(2)若二次函数y=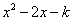 是闭区间[1,2]上的“闭函数”,求k的值;
是闭区间[1,2]上的“闭函数”,求k的值;
(3)若一次函数y=kx+b(k≠0)是闭区间[m,n]上的“闭函数”,求此函数的表达式(用含
m,n的代数式表示).
解:(1)反比例函数y=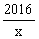 是闭区间[1,2016]上的“闭函数”.1分
是闭区间[1,2016]上的“闭函数”.1分
理由如下:
反比例函数y=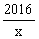 在第一象限,y随x的增大而减小,
在第一象限,y随x的增大而减小,
当x=1时,y=2016;…………………………………2分
当x=2016时,y=1,
即图象过点(1,2016)和(2016,1)
∴当1≤x≤2016时,有1≤y≤2016,符合闭函数的定义,
∴反比例函数y=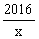 是闭区间[1,2016]上的“闭函数”;………3分
是闭区间[1,2016]上的“闭函数”;………3分
(2)由于二次函数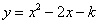 的图象开口向上,
的图象开口向上,
对称轴为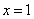 ,…………………………………………4分
,…………………………………………4分
∴二次函数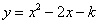 在闭区间[1,2]内,y随x的增大而增大.
在闭区间[1,2]内,y随x的增大而增大.
当x=1时,y=1,
∴k=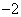 .
.
当x=2时,y=2,
∴k=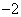 .
.
即图象过点(1,1)和(2,2)
∴当1≤x≤2时,有1≤y≤2,符合闭函数的定义,
∴k=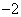 .…………………………………………………5分
.…………………………………………………5分
(3)因为一次函数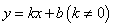 是闭区间
是闭区间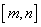 上的“闭函数”,
上的“闭函数”,
根据一次函数的图象与性质,有:
(Ⅰ)当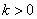 时,即图象过点(m,m)和(n,n)
时,即图象过点(m,m)和(n,n)
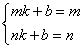 ,……………………………………………6分
,……………………………………………6分
解得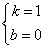 .
.
∴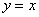 …………………………………………………7分
…………………………………………………7分
(Ⅱ)当 时,即图象过点(m,n)和(n,m)
时,即图象过点(m,n)和(n,m)
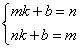 ,解得
,解得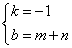
∴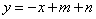 ,…………………………………8分
,…………………………………8分
∴一次函数的表达式为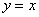 或
或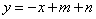 .
.

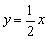 与双曲线
与双曲线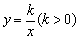 交于点A,B两点,点A的横坐标为4.
交于点A,B两点,点A的横坐标为4.
 .
.


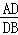 =__________.
=__________.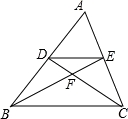

 B.BE=CF C.AC∥DF D.∠ACB=∠DEF
B.BE=CF C.AC∥DF D.∠ACB=∠DEF