题目内容
把二次函数的表达式y=x2﹣4x+6化为y=a(x﹣h)2+k的形式,那么h+k= .
4 .
【考点】二次函数的三种形式.
【分析】本题是将一般式化为顶点式,由于二次项系数是1,只需加上一次项系数的一半的平方来凑成完全平方式,从而得出h,k的值,进而求出h+k的值.
【解答】解:∵y=x2﹣4x+6=x2﹣4x+4﹣4+6=(x﹣2)2+2,
∴h=2,k=2,
∴h+k=2+2=4.
故答案为4.
【点评】本题考查了二次函数解析式的三种形式:
(1)一般式:y=ax2+bx+c(a≠0,a、b、c为常数);
(2)顶点式:y=a(x﹣h)2+k;
(3)交点式(与x轴):y=a(x﹣x1)(x﹣x2).

练习册系列答案
 优生乐园系列答案
优生乐园系列答案 新编小学单元自测题系列答案
新编小学单元自测题系列答案
相关题目
(1)抛物线m1:y1=a1x2+b1x+c1中,函数y1与自变量x之间的部分对应值如表:
| x | … | ﹣2 | ﹣1 | 1 | 2 | 4 | 5 | … |
| y1 | … | ﹣5 | 0 | 4 | 3 | ﹣5 | ﹣12 | … |
设抛物线m1的顶点为P,与y轴的交点为C,则点P的坐标为 ,点C的坐标为 .
(2)将设抛物线m1沿x轴翻折,得到抛物线m2:y2=a2x2+b2x+c2,则当x=﹣3时,y2= .
(3)在(1)的条件下,将抛物线m1沿水平方向平移,得到抛物线m3.设抛物线m1与x轴交于A,B两点(点A在点B的左侧),抛物线m3与x轴交于M,N两点(点M在点N的左侧).过点C作平行于x轴的直线,交抛物线m3于点K.问:是否存在以A,C,K,M为顶点的四边形是菱形的情形?若存在,请求出点K的坐标;若不存在,请说明理由.



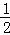 ∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
∠ABC,点D为直线BC上的动点,过点D作直线CM的垂线,垂足为E,交直线AC于F.
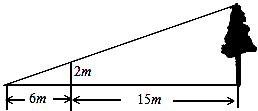

 轴对称的点的坐标是 .
轴对称的点的坐标是 .