题目内容
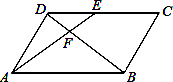
如图,在平行四边形ABCD中,E为CD上一点,连结AE,BD,且AE,BD交于点F,S△DEF:S△ABF=4:25,求DE:EC的值.
【考点】相似三角形的判定与性质;平行四边形的性质.
【分析】由四边形ABCD是平行四边形,可得△DEF∽△BAF,然后由相似三角形面积比等于相似比的平方,求得相似比,继而求得DE:EC的值.
【解答】解:∵四边形ABCD是平行四边形,
∴AB∥CD.
∴△DEF∽△BAF.
∴ .
.
∴ .
.
又∵AB=CD,
∴DE:EC=2:3.
【点评】此题考查了相似三角形的判定与性质以及平行四边形的性质.此题难度不大,注意掌握数形结合思想的应用.

练习册系列答案
 新题型全程检测期末冲刺100分系列答案
新题型全程检测期末冲刺100分系列答案
相关题目

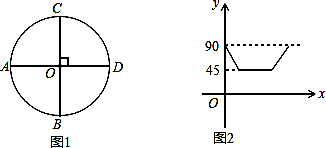

 ,求线段BD、BE与劣弧DE所围成的图形面积(结果保留根号和π).
,求线段BD、BE与劣弧DE所围成的图形面积(结果保留根号和π).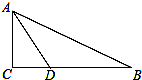
 B.
B. C.
C. D.
D.
 的两个实数根为x1、x2,
的两个实数根为x1、x2,