题目内容
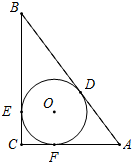如图，在△ABC中，∠C=90°，⊙O是△ABC的内切圆，切点分别为D，E，F，若BD=6，AD=4，求⊙O的半径r．考点：三角形的内切圆与内心
专题：
分析：利用切线的性质以及正方形的判定方法得出四边形OECF是正方形，进而利用勾股定理得出答案．
解答：
解：连接EO，FO，
∵⊙O是△ABC的内切圆，切点分别为D，E，F，
∴OE⊥BC，OF⊥AC，BD=BE，AD=AF，EC=CF，
又∵∠C=90°，
∴四边形ECFO是矩形，
又∵EO=FO，
∴矩形OECF是正方形，
设EO=x，
则EC=CF=x，
在Rt△ABC中
BC2+AC2=AB2
故（x+6）2+（x+4）2=102，
解得：x=2，
即⊙O的半径r=2．
解：连接EO，FO，∵⊙O是△ABC的内切圆，切点分别为D，E，F，
∴OE⊥BC，OF⊥AC，BD=BE，AD=AF，EC=CF，
又∵∠C=90°，
∴四边形ECFO是矩形，
又∵EO=FO，
∴矩形OECF是正方形，
设EO=x，
则EC=CF=x，
在Rt△ABC中
BC2+AC2=AB2
故（x+6）2+（x+4）2=102，
解得：x=2，
即⊙O的半径r=2．
点评：此题主要考查了三角形内切圆与内心，得出四边形OECF是正方形是解题关键．
练习册系列答案
相关题目
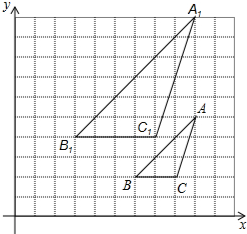如图，已知图中的每个小方格都是边长为1的小正方形，每个小正方形的顶点为格点．若△ABC与△A1B1C1是位似图形，且顶点都在格点上，请你画出位似中心点O，并写出位似中心的坐标（保留作图痕迹）．当x为任意实数时，下列分式一定有意义的是（ ）
A、
| ||
B、
| ||
C、
| ||
D、
|
如图，等腰△ABC的底边BC的长为2cm，面积是6cm2，腰AB的垂直平分线EF交AB于点E，交AC于点F．若D为BC边上的中点，M为线段EF上一动点，则△BDM的周长最短为