题目内容
5.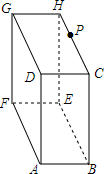 已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
分析 首先将长方体沿CH、HE、BE剪开,向右翻折,使面ABCD和面BEHC在同一个平面内,连接AM;或将长方体沿CH、C′D、C′H剪开,向上翻折,使面ABCD和面DCHC′在同一个平面内,连接AP,或将长方体沿AB、AF、EF剪开,向下翻折,使面CBEH和下面在同一个平面内,连接AP,然后分别在Rt△ADP与Rt△ABP与Rt△ACP,利用勾股定理求得AP的长,比较大小即可求得需要爬行的最短路程.
解答 解:将长方体沿CH、HE、BE剪开,向右翻折,使面ABCD和面BEHC在同一个平面内,连接AP,如图1,
由题意可得:PD=PC+CD=5+10=15cm,AD=20cm,
在Rt△ADP中,根据勾股定理得:AP=25cm;
将长方体沿CH、C′D、C′H剪开,向上翻折,使面ABCD和面DCHC′在同一个平面内,连接AP,
如图2,
由题意得:BP=BC+PC=5+20=25(cm),AB=10cm,
在Rt△ABP中,根据勾股定理得:AP=5$\sqrt{29}$cm,
连接AP,如图3,
由题意得:AC=AB+CB=10+20=30(cm),PC=5cm,
在Rt△ACP中,根据勾股定理得:AP=5 $\sqrt{37}$cm,
∵25<5$\sqrt{29}$$<5\sqrt{37}$,
则需要爬行的最短距离是25cm.
故答案为:25cm.
点评 此题考查了最短路径问题,利用了转化的思想,解题的关键是将立体图形展为平面图形,利用勾股定理的知识求解.

练习册系列答案
 课时训练江苏人民出版社系列答案
课时训练江苏人民出版社系列答案 黄冈经典趣味课堂系列答案
黄冈经典趣味课堂系列答案
相关题目
16.有15位同学参加学校组织的才艺表演比赛,已知他们所得的分数互不相同,共设8个获奖名额,某同学知道自己的比赛分数后,要判断自己能否获奖,在下列15位同学成绩的统计量中只需知道一个量,它是( )
| A. | 平均数 | B. | 众数 | C. | 中位数 | D. | 方差 |
13.如果把分数$\frac{ab}{a+b}$(a和b都不为0)中的a,b都扩大2倍,那么分式的值一定( )
| A. | 不变 | B. | 是原来的2倍 | C. | 是原来的3倍 | D. | 是原来的4倍 |
15.观察下面每一个图形中小圈圈的组合规律,可判断第15个图形中小圈圈的个数为( )

| A. | 451 | B. | 630 | C. | 631 | D. | 675 |
 将一张矩形的纸对折再折,然后沿着左图中的虚线剪下打开,你发现这是一个等腰梯形.
将一张矩形的纸对折再折,然后沿着左图中的虚线剪下打开,你发现这是一个等腰梯形. 一个粮仓如图,请您细心算出这个粮仓的容积是1.7π立方米.
一个粮仓如图,请您细心算出这个粮仓的容积是1.7π立方米.