题目内容
14. 一个粮仓如图,请您细心算出这个粮仓的容积是1.7π立方米.
一个粮仓如图,请您细心算出这个粮仓的容积是1.7π立方米.(参考公式:V圆柱=πr2h,V圆锥=$\frac{1}{3}$πr2h,结果保留π)
分析 先根据图形确定出圆锥和圆柱的底面半径和高,然后代入计算即可.
解答 解:根据题意可知:圆柱和圆锥的底面半径为r=1,圆锥的高h=0.6,圆柱的高h=1.5.
这个粮仓的容积=π×12×1.5+$\frac{1}{3}$π×12×0.6
=1.5π+0.2π
=1.7π.
故答案为:1.7π.
点评 本题主要考查的是求代数式的值,判断出圆柱和圆锥的底面半径和高的长度是解题的关键.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5.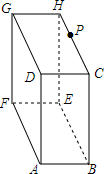 已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
 已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
2.如果分式$\frac{x-3}{2x+1}$有意义,则x的取值范围是( )
| A. | x≠3 | B. | x$≠-\frac{1}{2}$ | C. | x=-$\frac{1}{2}$ | D. | x=3 |
19.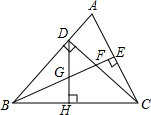 已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )
 已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )
已知,如图△ABC中,∠ABC=45°,CD⊥AB于D,BE平分∠ABC,且BE⊥AC于E,与CD相交于点F,H是BC边的中点,连接DH与BE相交于点G,某同学分析图形后得出以下结论:①DH⊥BC;②CE=$\frac{1}{2}BF$;③△AEB≌△CEB;④△BDF≌△CDA.上述结论一定正确的是( )| A. | ①③ | B. | ③④ | C. | ①③④ | D. | ①②③④ |
6. 观察表格:
观察表格:
根据表格解答下列问题:
(1)a=1,b=-2,c=-3;
(2)画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c>0成立.
 观察表格:
观察表格:| X | 0 | 1 | 2 |
| ax | 0 | 1 | 2 |
| ax2+bx+c | -3 | -4 | -3 |
(1)a=1,b=-2,c=-3;
(2)画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c>0成立.
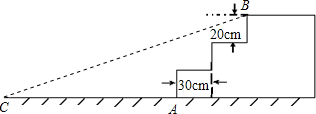 奥运会期间,某公园入口处原有三级台阶,为方便残疾人士,拟将台阶改为斜坡,每级台阶高为20cm,深为30cm.设台阶的起点为A,斜坡的起始点为C,现将斜坡的坡角∠BCA设计为12°,求AC的长度.(参考数据:tan12°=$\frac{3}{14}$)
奥运会期间,某公园入口处原有三级台阶,为方便残疾人士,拟将台阶改为斜坡,每级台阶高为20cm,深为30cm.设台阶的起点为A,斜坡的起始点为C,现将斜坡的坡角∠BCA设计为12°,求AC的长度.(参考数据:tan12°=$\frac{3}{14}$)