题目内容
20.计算(1)($\frac{1}{2}$)-1+($\sqrt{3}$-$\sqrt{2}$)0+|-3|
(2)(x+2y)2-(x+y)(x-y)
(3)$\frac{a}{a-x}$+$\frac{x}{x-a}$
(4)$\frac{a-1}{{a}^{2}-1}$-$\frac{a}{a+1}$.
分析 (1)原式利用零指数幂、负整数指数幂法则,以及绝对值的代数意义化简即可得到结果;
(2)原式利用完全平方公式及平方差公式化简,去括号合并即可得到结果;
(3)原式变形后,利用同分母分式的减法法则计算即可得到结果;
(4)原式通分并利用同分母分式的减法法则计算即可得到结果.
解答 解:(1)原式=2+1+3=6;
(2)原式=x2+4xy+4y2-x2+y2=4xy+5y2;
(3)原式=$\frac{-a}{x-a}$+$\frac{x}{x-a}$=$\frac{x-a}{x-a}$=1;
(4)原式=$\frac{a-1-a(a-1)}{(a+1)(a-1)}$=$\frac{-(a-1)^{2}}{(a+1)(a-1)}$=-$\frac{a-1}{a+1}$.
点评 此题考查了分式的加减法,以及实数的运算,熟练掌握运算法则是解本题的关键.

练习册系列答案
相关题目
11.如图,铅笔放置在△ABC的边AB上,笔尖方向为点A到点B的方向,把铅笔依次绕点A、点C、点B按逆时针方向旋转∠A、∠C、∠B的度数后,笔尖方向变为点B到点A的方向,这种变化说明( )


| A. | 三角形内角和等于180° | B. | 三角形外角和等于360° | ||
| C. | 三角形任意两边之和大于第三边 | D. | 三角形任意两边之差小于第三边 |
15.合肥市有400万人口,在一次对城市未来建设方案的民意调查中,随机调查了4万人,其中有2.1万人同意甲方案,则由此可估计该城市中,同意甲方案的大约有多少万人( )
| A. | 3 | B. | 2.1 | C. | 210 | D. | 无法统计 |
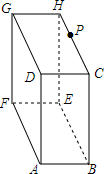 已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.