题目内容
15.观察下面每一个图形中小圈圈的组合规律,可判断第15个图形中小圈圈的个数为( )
| A. | 451 | B. | 630 | C. | 631 | D. | 675 |
分析 由图形可知:第1个图形中小圈圈的个数为1,第2个图形中小圈圈的个数为1+6=7,第3个图形中小圈圈的个数为1+1×6+2×6=19,第4个图形中小圈圈的个数为1+1×6+2×6+3×6=37,…由此得出第n个图形中小圈圈的个数为1+1×6+2×6+3×6+…+6(n-1)=1+6(1+2+3+…+n-1)=1+6×$\frac{1}{2}$n(n-1)=3n(n-1)+1,进一步代入求得答案即可.
解答 解:∵第1个图形中小圈圈的个数为1,
第2个图形中小圈圈的个数为1+6=7,
第3个图形中小圈圈的个数为1+1×6+2×6=19,
第4个图形中小圈圈的个数为1+1×6+2×6+3×6=37,
…
∴第n个图形中小圈圈的个数为1+1×6+2×6+3×6+…+6(n-1)=1+6(1+2+3+…+n-1)=1+6×$\frac{1}{2}$n(n-1)=3n(n-1)+1,
∴第15个图形中小圈圈的个数为3×15×14+1=631.
故选:C.
点评 此题考查图形的变化规律,找出图形之间的联系,得出数字之间的运算规律,利用规律解决问题.

练习册系列答案
相关题目
5.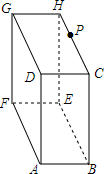 已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
 已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
已知一个长方体纸箱按如图方式摆放,其中AB=10cm,AF=15cm,AD=20cm,点P在CH上,且CP=5cm,一只蚂蚁如果要沿着长方体纸箱的表面从点A爬到点P,需要爬行的最短距离是25cm.
6. 观察表格:
观察表格:
根据表格解答下列问题:
(1)a=1,b=-2,c=-3;
(2)画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c>0成立.
 观察表格:
观察表格:| X | 0 | 1 | 2 |
| ax | 0 | 1 | 2 |
| ax2+bx+c | -3 | -4 | -3 |
(1)a=1,b=-2,c=-3;
(2)画出函数y=ax2+bx+c的图象,并根据图象,直接写出当x取什么实数时,不等式ax2+bx+c>0成立.