题目内容
5.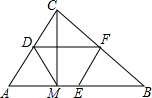 如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.
如图,已知D、E、F为△ABC的三边的中点,CM⊥AB.(1)若EF=6,则DM的长度为6;
(2)四边形DMEF是什么样的四边形?等腰梯形 (填出其不同于一般四边形主要特点也可).
分析 (1)先根据三角形的中位线定理可得:EF=$\frac{1}{2}$AC,然后根据直角三角形的中线等于斜边的一半可得:DM=$\frac{1}{2}$AC,从而可得DM=EF=6;
(2)先证明四边形DMEF是梯形,再证明其两腰相等即可证明四边形DMEF是等腰梯形.
解答 (1)解:∵E、F分别边AC,BC的中点,
∴EF=$\frac{1}{2}$AC,
∵CM是BA边上的高,
∴△ACM是直角三角形,
∵D是AC的中点,
∴DM=$\frac{1}{2}$AC,
∴EF=DM,
∵EF=6,
∴DM=6;
(2)证明:∵D、F分别为边AC,AB的中点,
∴DF∥BA即DF∥ME,
∵DF=AE=$\frac{1}{2}$BA≠ME,
∴四边形DMEF是梯形,
∵EF=DM,
∴四边形DMEF是等腰梯形.
故答案为:6;等腰梯形.
点评 此题考查了三角形的中位线定理,直角三角形的中线的性质及等腰梯形的判定方法,解题的关键是:利用三角形的中位线定理及直角三角形的中线的性质证明DM=EF.

练习册系列答案
相关题目
15.将点A(-1,2)沿x轴向右平移3个单位长度,再沿y轴向下平移4个单位长度后得到点A′的坐标为( )
| A. | (-4,-2 ) | B. | (2,-2 ) | C. | (-4,6 ) | D. | (2,6 ) |
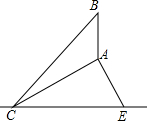 如图,CE为水平线,斜坡AC的坡度(坡比)为1:$\sqrt{3}$,AC=10米,坡顶有一直立旗杆BA,现在想用一根彩带从旗杆顶端B点连接到坡底C点,如果已知旗杆AB长为3米,试求彩带BC至少准备多长?
如图,CE为水平线,斜坡AC的坡度(坡比)为1:$\sqrt{3}$,AC=10米,坡顶有一直立旗杆BA,现在想用一根彩带从旗杆顶端B点连接到坡底C点,如果已知旗杆AB长为3米,试求彩带BC至少准备多长?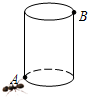 如图,有一个底边半径为6cm,高为24cm的圆柱,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与A点相对的B处的食物,试问:它需要爬行的最短路程越是多少?
如图,有一个底边半径为6cm,高为24cm的圆柱,在圆柱下底面的点A处有一只蚂蚁,它想吃到上底面上与A点相对的B处的食物,试问:它需要爬行的最短路程越是多少?