题目内容
15.已知一次函数y1=kx+b的图象与反比例函数y2=$\frac{k-6}{x}$的图象相交,其中一个交点的横坐标为-1,另一个交点的横坐标为-2.(1)求这两个函数的解析式;
(2)画出这两个函数的图象;
(3)结合图象填空:
①y1≥y2时,x的取值范围是-2≤x≤-1或x>0;
②当x≤-2时,y2的取值范围是0<y≤2.
分析 (1)由题意得$\left\{\begin{array}{l}{-k+b=-(k-6)}\\{-2k+b=-\frac{k-6}{2}}\end{array}\right.$,解方程组即可求得k、b的值,从而求得解析式;
(2)从正数,负数中各选几个值作为x的值,进而得到y的值,描点,连线即可画出反比例函数的图象,然后根据两点画出直线即可;
(3)根据图象即可求得.
解答 解:(1)由题意得$\left\{\begin{array}{l}{-k+b=-(k-6)}\\{-2k+b=-\frac{k-6}{2}}\end{array}\right.$
解得$\left\{\begin{array}{l}{k=2}\\{b=6}\end{array}\right.$,
∴这两个函数的解析式为y1=2x+6,y2=-$\frac{4}{x}$;
(2)画出这两个函数的图象如图: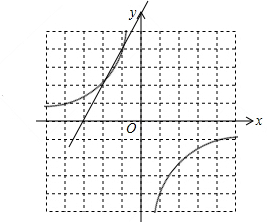
(3)由图象可知:
①-2≤x≤-1或x>0;
②0<y≤2.
故答案为:-2≤x≤-1;0<y≤2.
点评 本题考查了反比例函数和一次函数的交点问题以及画出函数的图象;根据题意列出方程组是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
3.为了鼓励市民节约用水,某市居民生活用水按阶梯式水价计费.下表是该市居民“一户一表”生活用水阶梯式计费价格表的一部分信息:
(说明:①每户产生的污水量等于该户的用水量,②水费=自来水费+污水处理费)已知小明家2014年4月份用水20吨,交水费66元;5月份用水35吨,交水费150元.
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民6月用水27吨,其当月交水费多少元?
| 用户每月用水量 | 自来水单价(元/吨) | 污水处理费用(元/吨) |
| 17吨及以下 | a | 0.80 |
| 超过17吨不超过30吨的部分 | b | 0.80 |
| 超过30吨的部分 | 6.00 | 0.80 |
(1)求a、b的值.
(2)实行“阶梯水价”收费之后,该市一户居民6月用水27吨,其当月交水费多少元?
7.计算[-2(-xn-1)]3=( )
| A. | -2x3n-1 | B. | 8x3n-3 | C. | 16x3n-3 | D. | -16x3n-3 |
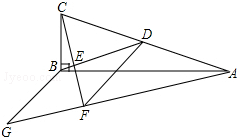 如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若FG=5,CF=6,则四边形BDFG的面积为15.
如图,在△ABC中,∠ABC=90°,BD为AC的中线,过点C作CE⊥BD于点E,过点A作BD的平行线,交CE的延长线于点F,在AF的延长线上截取FG=BD,连接BG、DF.若FG=5,CF=6,则四边形BDFG的面积为15.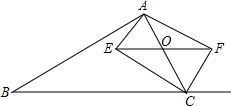 如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F
如图,在△ABC中,点O是AC边上一动点,过点O作BC的平行线交∠ACB的角平分线于点E,交∠ACB的外角平分线于点F