题目内容
17.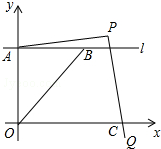 如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.
如图,在平面直角坐标系中,直线l平行x轴,交y轴于点A,第一象限内的点B在l上,连结OB,动点P满足∠APQ=90°,PQ交x轴于点C.(1)当动点P与点B重合时,若点B的坐标是(2,1),求PA的长.
(2)当动点P在线段OB的延长线上时,若点A的纵坐标与点B的横坐标相等,求PA:PC的值;
(3)在(2)的条件下,已知AB=3,OB:BP=3:1,求四边形AOCP的面积.
分析 (1)易得点P的坐标是(2,1),即可得到PA的长.
(2)易证∠AOB=45°,由角平分线的性质可得PM=PN,然后通过证明△ANP≌△CMP即可求出PA:PC的值.
(3)易证四边形OMPN为正方形,利用AB=3,OB:BP=3:1,求出对角线OP的长,再求出S正方形OMPN,利用三角形全等,进行等积变换,S四边形AOCO=S正方形OMPN.
解答 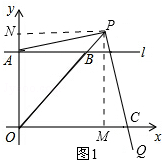 解:(1)∵点P与点B重合,点B的坐标是(2,1),
解:(1)∵点P与点B重合,点B的坐标是(2,1),
∴点P的坐标是(2,1).
∴PA的长为2.
(2)过点P作PM⊥x轴,垂足为M,过点P作PN⊥y轴,垂足为N,如图1所示.
∵点A的纵坐标与点B的横坐标相等,
∴OA=AB.
∵∠OAB=90°,
∴∠AOB=∠ABO=45°.
∵∠AOC=90°,
∴∠POC=45°.
∵PM⊥x轴,PN⊥y轴,
∴PM=PN,∠ANP=∠CMP=∠OMP=90°.
∴∠NPM=90°.
∵∠APC=90°.
∴∠APN=90°-∠APM=∠CPM.
在△ANP和△CMP中,
∵∠APN=∠CPM,PN=PM,∠ANP=∠CMP,
∴△ANP≌△CMP.
∴PA=PC.
∴PA:PC的值为1:1.
(3)∵∠ANP=∠MON=∠OMP=90°
∴四边形OMPN为矩形
∵PM=PN
∴四边形OMPN为正方形
∵∠OAB=90°,OA=AB=3
∴OB=$3\sqrt{2}$
∵OB:BP=3:1
∴BP=$\sqrt{2}$
∴OP=$4\sqrt{2}$
∴S正方形OMPN=$\frac{{{{({4\sqrt{2}})}^2}}}{2}=16$
∵△ANP≌△CMP.
∴S△ANP≌S△CMP.
∴S四边形AOCO=S正方形OMPN=16.
点评 本题考查了角平分线的性质、全等三角形的判定与性质、矩形和正方形的判定与性质、等腰三角形的判定与性质、勾股定理,等积变换等知识,综合性较强.

| A. | -1 | B. | -3 | C. | 1 | D. | 3 |
| A. | 4.15×107 | B. | 4.15×108 | C. | 41.5×107 | D. | 41.5×108 |
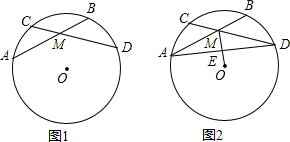
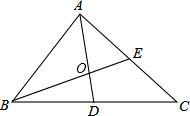 如图,在△ABC中,中线AD、BE交于O,若S△BOD=5,则S△BOA=10.
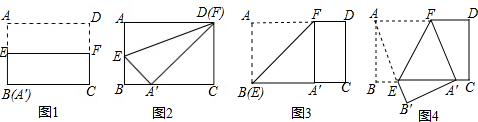
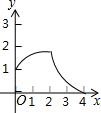
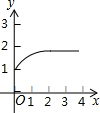
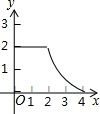
如图,在△ABC中,中线AD、BE交于O,若S△BOD=5,则S△BOA=10.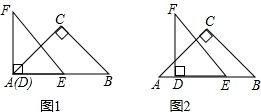 如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )
如图1,△ABC和△DEF都是等腰直角三角形,其中∠C=∠EDF=90°,点A与点D重合,点E在AB上,AB=4,DE=2.如图2,△ABC保持不动,△DEF沿着线段AB从点A向点B移动,当点D与点B重合时停止移动.设AD=x,△DEF与△ABC重叠部分的面积为y,则y关于x的函数图象大致是( )
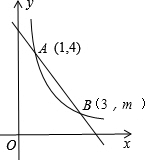 如图,在直角坐标系xOy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点.
如图,在直角坐标系xOy中,一次函数y1=k1x+b的图象与反比例函数y2=$\frac{{k}_{2}}{x}$的图象交于A(1,4),B(3,m)两点.