题目内容
20.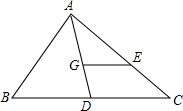 如图,点G是△ABC的重心,GE∥BC,如果BC=12,那么线段GE的长为4.
如图,点G是△ABC的重心,GE∥BC,如果BC=12,那么线段GE的长为4.
分析 先根据三角形重心性质得到AG=2GD,AD=CD=$\frac{1}{2}$BC=6,再证明△AGE∽△ADC,然后利用相似比可计算GE的长.
解答 解:∵点G是△ABC的重心,
∴AD为中线,AG=2GD,
∴AD=CD=$\frac{1}{2}$BC=6,
∵GE∥BC,
∴△AGE∽△ADC,
∴$\frac{AG}{AD}$=$\frac{GE}{DC}$,即$\frac{GE}{6}$=$\frac{2}{3}$,
∴GE=4.
故答案为4.
点评 本题考查了相似三角形的判定与性质:两个三角形相似对应角相等,对应边的比相等.在判定两个三角形相似时,应注意利用图形中已有的公共角、公共边等隐含条件,以充分发挥基本图形的作用,寻找相似三角形的一般方法是通过作平行线构造相似三角形.解决本题的关键是理解三角形重心的性质.

练习册系列答案
相关题目
11.一个圆锥的侧面展开图是半径为8,圆心角为120°的扇形,则这个圆锥的高为( )
| A. | $\frac{16}{3}\sqrt{2}$cm | B. | $\frac{16}{3}$cm | C. | $\frac{8}{3}\sqrt{2}$cm | D. | $\frac{8}{3}$cm |
15.若等腰三角形的两边长为3和7,则该等腰三角形的周长为( )
| A. | 10 | B. | 13 | C. | 17 | D. | 13或17 |
 如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$.
如图,在边长为5cm的正方形纸片ABCD中,点F在边BC上,已知FB=2cm.如果将纸折起,使点A落在点F上,则tan∠GEA=$\frac{5}{2}$. 如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50°,则∠B=130°.
如图,已知四边形ABCD内接于⊙O,点O在∠D的内部,∠OAD+∠OCD=50°,则∠B=130°.
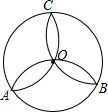 如图,在A处有两只蚂蚁,一只从A出发,沿圆过B,C回到A,另一只则从A到O,到B,再从另一条线回到O,到C,再沿圆(不过B)回到A.如果两只蚂蚁爬得一样快,哪只蚂蚁先回到A处?为什么?
如图,在A处有两只蚂蚁,一只从A出发,沿圆过B,C回到A,另一只则从A到O,到B,再从另一条线回到O,到C,再沿圆(不过B)回到A.如果两只蚂蚁爬得一样快,哪只蚂蚁先回到A处?为什么? 如图,直线AB、CD交于点O,∠AOE=150°,且OE平分∠DOB,则∠AOC=60度.
如图,直线AB、CD交于点O,∠AOE=150°,且OE平分∠DOB,则∠AOC=60度.