题目内容
8.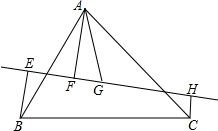 如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF.
如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF.
分析 连接AG,并延长,交BC于D,过D做DK垂直于直线L,垂足为K,根据三角形中线的性质得到BD=CD,推出BE∥DK∥CH,得到DK为梯开EBCH的中线,求得DK=$\frac{1}{2}$(BE+CH),根据相似三角形的性质得到$\frac{AF}{DK}=\frac{AG}{DG}$=$\frac{1}{2}$,得到AF=2DK,根据得到结论.
解答  证明:连接AG,并延长,交BC于D,过D做DK垂直于直线L,垂足为K,
证明:连接AG,并延长,交BC于D,过D做DK垂直于直线L,垂足为K,
∵直线l过△ABC的重心G,
∴BD=CD,
∵BE⊥直线l,CH⊥直线l,DK⊥直线l,
∴BE∥DK∥CH,
∴DK为梯开EBCH的中线,
∴DK=$\frac{1}{2}$(BE+CH),
∵AF⊥直线l,
∴AF∥DK,
∴△AFG∽△DKG,
∴$\frac{AF}{DK}=\frac{AG}{DG}$=$\frac{1}{2}$,
∴AF=2DK,
∴AF=BE+CH.
点评 本题考查了三角形的重心,相似三角形的判定和性质,梯形的中位线的性质,正确的作出辅助线是解题的关键.

练习册系列答案
 科学实验活动册系列答案
科学实验活动册系列答案
相关题目
20.已知A(-5,m2),B(-2,a),C(-0.5,b),D(4,c)都在反比例函数y=$\frac{k}{x}$的图象上,则下列判断正确的是( )
| A. | m2最大 | B. | a最大 | C. | b最大 | D. | c最大 |

 如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.
如图,已知四边形ABCD内接于⊙O,直径AC=6,对角线AC、BD交于E点,且AB=BD,EC=1,则AD的长是$\frac{3\sqrt{15}}{2}$.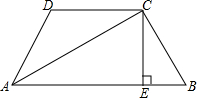 已知:四边形ABCD中,∠B+∠D=180°,AC平分∠BAD,点E在AB上,满足∠ADC-∠ABC=2∠BCE,求证:CE⊥AB.
已知:四边形ABCD中,∠B+∠D=180°,AC平分∠BAD,点E在AB上,满足∠ADC-∠ABC=2∠BCE,求证:CE⊥AB.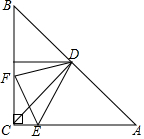 已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.
已知△ACB为等腰直角三角形,D为BA的中点,∠EDF=45°,交AC于E点,交BC于F点,连EF.