题目内容
5.将下列连分式中的a,b,c,d用2,3,4,5四个数不重复的任意替换,a+$\frac{1}{b+\frac{1}{c+\frac{1}{d}}}$,则此连分数的最大值是5$\frac{13}{30}$.分析 由于a,b,c,d用2,3,4,5四个数不重复的任意替换,将a+$\frac{1}{b+\frac{1}{c+\frac{1}{d}}}$变形为5+$\frac{1}{2+\frac{1}{3+\frac{1}{4}}}$,计算可求此连分数的最大值.
解答 解:∵a,b,c,d用2,3,4,5四个数不重复的任意替换,
∴a+$\frac{1}{b+\frac{1}{c+\frac{1}{d}}}$的最大值为5+$\frac{1}{2+\frac{1}{3+\frac{1}{4}}}$=5+$\frac{1}{2+\frac{1}{\frac{13}{4}}}$=5+$\frac{1}{2+\frac{4}{13}}$=5+$\frac{1}{\frac{30}{13}}$=5+$\frac{13}{30}$=5$\frac{13}{30}$.
故答案为:5$\frac{13}{30}$.
点评 此题考查了有理数,关键是将a+$\frac{1}{b+\frac{1}{c+\frac{1}{d}}}$变形为5+$\frac{1}{2+\frac{1}{3+\frac{1}{4}}}$.

练习册系列答案
相关题目

 如图,正三角形ABC内接于⊙O,AD是⊙O的内接正十二边形的一条边,若CD的长为5$\sqrt{2}$,则⊙O的半径为5.
如图,正三角形ABC内接于⊙O,AD是⊙O的内接正十二边形的一条边,若CD的长为5$\sqrt{2}$,则⊙O的半径为5. 如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6,
如图,在△ABC中,∠B=∠AED,AB=5,AD=3,CE=6, 根据立体图从上面看到的形状图(如图所示),画出它从正面和左面看到的形状图(图中数字代表该位置的小正方体的个数).
根据立体图从上面看到的形状图(如图所示),画出它从正面和左面看到的形状图(图中数字代表该位置的小正方体的个数).
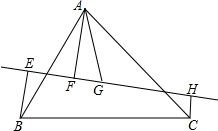 如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF.
如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF.