题目内容
6.如图①,△ABC的角平分线BD,CE相交于点P.
(1)如果∠A=80°,求∠BPC的度数;
(2)如图②,过P点作直线MN,分别交AB和AC于点M和N,探索∠MPB,∠NPC,∠A三者之间的数量关系,并加以证明;
(3)将直线MN绕点P旋转,使MN与AC的交点在AC的延长线上,如图③,∠MPB,∠NPC,∠A三者之间又有怎样的数量关系?
分析 (1)根据三角形内角和定理得到∠BPC=180°-∠PBC-∠PCB,再根据角平分线定义得到∠BPC=180°-($\frac{1}{2}$∠ABC+$\frac{1}{2}$∠ACB),再利用三角形内角和定理得∠BPC=180°-$\frac{1}{2}$(180°-∠A)=90°+$\frac{1}{2}$∠A,然后把∠A的度数代入计算;
(2)如图③,结论:∠MPB+∠NPC=90°-$\frac{1}{2}$∠A.根据平角定义得∠MPB+∠NPC=180°-∠BPC,然后根据(1)的求解;
(3)不成立,结论是:∠MPB-∠NPC=90°-$\frac{1}{2}$∠A.由∠MPB=180°-∠BPN=180°-(∠BPC-∠NPC),推出∠MPB-∠NPC=180°-∠BPC=180°-(90°+$\frac{1}{2}$∠A),由此即可证明.
解答 解:(1)如图①
∵在△ABC中,∠A+∠B+∠ACB=180°,且∠A=80°,
∴∠ABC+∠ACB=100°,
∵∠1=$\frac{1}{2}$∠ABC,∠2=$\frac{1}{2}$∠ACB,
∴∠1+∠2=$\frac{1}{2}$(∠ABC+∠ACB)=$\frac{1}{2}$×100°=50°,
∴∠BPC=180°-(∠1+∠2)=180°-50°=130°.
(2)如图③,结论:∠MPB+∠NPC=90°-$\frac{1}{2}$∠A.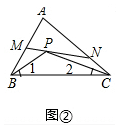
理由:由(1)知:∠BPC=180°-(∠1+∠2);
∵∠1+∠2=$\frac{1}{2}$(180°-∠A)=90°-$\frac{1}{2}$∠A,
∴∠BPC=180°-(90°-$\frac{1}{2}$∠A)=90°+$\frac{1}{2}$∠A;
∴∠MPB+∠NPC=180°-∠BPC=180°-(90°+$\frac{1}{2}$∠A)=90°-$\frac{1}{2}$∠A.
(3)不成立,结论是:∠MPB-∠NPC=90°-$\frac{1}{2}$∠A.
如图③
理由:由(ⅰ)知:∠BPC=90°+$\frac{1}{2}$∠A,
∵∠MPB=180°-∠BPN=180°-(∠BPC-∠NPC),
∴∠MPB-∠NPC=180°-∠BPC=180°-(90°+$\frac{1}{2}$∠A)=90°-$\frac{1}{2}$∠A.
点评 该题主要考查了三角形的内角和定理、角平分线的定义等几何知识点及其应用问题;牢固掌握三角形的内角和定理、角平分线的定义等几何知识点是基础,灵活运用是关键.

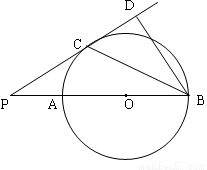
 如图,正三角形ABC内接于⊙O,AD是⊙O的内接正十二边形的一条边,若CD的长为5$\sqrt{2}$,则⊙O的半径为5.
如图,正三角形ABC内接于⊙O,AD是⊙O的内接正十二边形的一条边,若CD的长为5$\sqrt{2}$,则⊙O的半径为5.
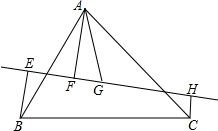 如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF.
如图,直线l过△ABC的重心G,它与两边AB、AC相交,设A,B,C在l上的射影分别是F,E,H,求证:BE+CH=AF. 如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.
如图,在边长为1的正方形组成的6×5方格中,点A,B都在格点上.