题目内容
18. 如图,在△ABC中,AB=8,AC=6,AD=12,点D在BC的延长线上,且△ACD∽△BAD,求BD的长.
如图,在△ABC中,AB=8,AC=6,AD=12,点D在BC的延长线上,且△ACD∽△BAD,求BD的长.
分析 由△ACD∽△BAD,根据相似三角形的对应边成比例,可得$\frac{AD}{BD}=\frac{AC}{AB}$,继而求得答案.
解答 解:∵△ACD∽△BAD,
∴$\frac{AD}{BD}=\frac{AC}{AB}$,
∵AB=8,AC=6,AD=12,
∴$\frac{12}{BD}=\frac{6}{8}$,
解得:BD=16.
点评 此题考查了相似三角形的性质.注意相似三角形的对应边成比例.

练习册系列答案
相关题目
13.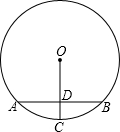 如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
 如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )
如图,O是圆心,半径OC⊥弦AB于点D,AB=8,OD=3,则CD等于( )| A. | 2 | B. | 3 | C. | 2$\sqrt{2}$ | D. | 2$\sqrt{3}$ |
8. 如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为( )
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为( )
 如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为( )
如图,△ABC≌△ADE,若∠B=80°,∠C=30°,则∠EAD的度数为( )| A. | 80° | B. | 70° | C. | 30° | D. | 110° |
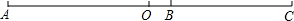 如图:AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度.(括号内注理由)
如图:AB=4cm,BC=3cm,如果O是线段AC的中点,求线段OB的长度.(括号内注理由)
 如图,四边形ABCD内接于⊙O,∠ABC=140°,则∠AOC的度数为80°.
如图,四边形ABCD内接于⊙O,∠ABC=140°,则∠AOC的度数为80°.