题目内容
9. 如图,四边形ABCD内接于⊙O,∠ABC=140°,则∠AOC的度数为80°.
如图,四边形ABCD内接于⊙O,∠ABC=140°,则∠AOC的度数为80°.
分析 由四边形ABCD内接于⊙O,∠ABC=140°,根据圆的内接四边形的对角互补,即可求得∠D的度数,又由圆周角定理,即可求得答案.
解答 解:∵四边形ABCD内接于⊙O,∠ABC=140°,
∴∠D=180°-∠ABC=40°,
∴∠AOC=2∠D=80°.
故答案为:80°.
点评 此题考查了圆的内接四边形的性质以及圆周角定理.注意圆内接四边形的对角互补.

练习册系列答案
相关题目
4.下列等式成立的是( )
| A. | (-$\frac{2}{3}$)-2=$\frac{4}{9}$ | B. | $\frac{-a+b}{c}$=-$\frac{a+b}{c}$ | ||
| C. | 0.00061=6.1×10-5 | D. | $\frac{-a-b}{-a+b}$=$\frac{a+b}{a-b}$ |
19.下列各组数据中,结果相等的是( )
| A. | (-1)4与-14 | B. | -|-3|与-(-3) | C. | ${\frac{2}{3}^2}与{({\frac{2}{3}})^2}$ | D. | ${({\frac{-1}{3}})^3}与\frac{-1}{3^3}$ |
 如图,在△ABC中,AB=8,AC=6,AD=12,点D在BC的延长线上,且△ACD∽△BAD,求BD的长.
如图,在△ABC中,AB=8,AC=6,AD=12,点D在BC的延长线上,且△ACD∽△BAD,求BD的长.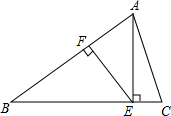 已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,若CE=2,cos∠AEF=$\frac{4}{5}$,求BE的长.
已知:如图,等腰△ABC中,AB=BC,AE⊥BC于E,EF⊥AB于F,若CE=2,cos∠AEF=$\frac{4}{5}$,求BE的长.