题目内容
5. 小明家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形猪圈,如图所示,一面墙的中间留出1米宽的进出门(门使用另外的材料).现备有足够砌15米长的围墙的材料,设猪圈与已有墙面垂直的墙的长度为x米.
小明家想利用房屋侧面的一面墙,再砌三面墙,围成一个矩形猪圈,如图所示,一面墙的中间留出1米宽的进出门(门使用另外的材料).现备有足够砌15米长的围墙的材料,设猪圈与已有墙面垂直的墙的长度为x米.(1)要使猪圈面积为24平方米,如何设计三面围墙的长度.
(3)能否使猪圈面积为36平方米?说明理由.
分析 (1)设猪圈与已有墙面垂直的墙的长度为x米,则与已有墙面平行的墙的长度为(15+1-2x)米,根据面积为24,列方程求解;
(2)令面积为36,列方程求解进行判断.
解答 解:(1)设猪圈与已有墙面垂直的墙的长度为x米,则与已有墙面平行的墙的长度为(15+1-2x)米,
由题意得,(15+1-2x)x=24,
解得:x1=2,x2=6,
当x1=2时,16-2x=12,
当x2=6时,16-2x=4,
答:猪圈与已有墙面垂直的墙的长度为2米,与已有墙面平行的墙的长度为12米,
或猪圈与已有墙面垂直的墙的长度为6米,则与已有墙面平行的墙的长度为4米;
(2)当面积为36平方米时,
(15+1-2x)x=36,
此时无解.
答:不能使猪圈面积为36平方米.
点评 本题考查了一元二次方程的应用,解答本题的关键是读懂题意,设出未知数,找出合适的等量关系,列方程求解.

练习册系列答案
相关题目
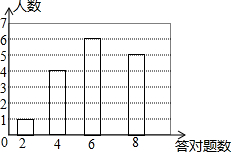 计算机网络知识竞赛,答对1题得10分,某次竞赛结果如图所示(每位参赛选手至少答对2题)
计算机网络知识竞赛,答对1题得10分,某次竞赛结果如图所示(每位参赛选手至少答对2题)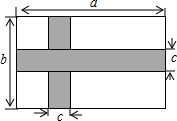 如图,有一块长为a米,宽为b米的长方形地块,规划部门计划将阴影部分修成宽度为c米的小路,其余部分进行绿化,则阴影部分的面积是多少平方米?并求出当a=5,b=3,c=1时阴影部分的面积.
如图,有一块长为a米,宽为b米的长方形地块,规划部门计划将阴影部分修成宽度为c米的小路,其余部分进行绿化,则阴影部分的面积是多少平方米?并求出当a=5,b=3,c=1时阴影部分的面积.