题目内容
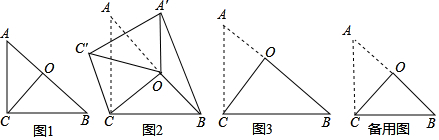
11.已知:如图1,点P在线段AB上(AP>PB),C、D、E分别是AP、PB、AB的中点,正方形CPFG和正方形PDHK在直线AB同侧.(1)求证:GC=ED
(2)求证:△EHG是等腰直角三角形;
(3)若将图1中的射线PB连同正方形PDHK绕点P顺时针旋转一个角度后,其它已知条件不变,如图2,判断△EHG还是等腰直角三角形吗?若是,给予证明;若不是,请说明理由.

分析 (1)由先根据C、D、E分别是AP、PB、AB的中点,易证得CE=DP,继而可证得CP=DE,然后由四边形CPFG和四边形PDHK都是正方形,证得结论;
(2)由四边形CPFG和四边形PDHK都是正方形,易得CE=DP=DH,CG=CP=DE,∠GCE=∠EDH=90°,然后由全等三角形的判定定理求出△CEG≌△DHE,由直角三角形的两锐角互补即可解答;
(3)连接CE、ED,根据三角形中位线定理及直角三角形的性质可得?CEDP,再由CE=DP=DH,CG=CP=DE,∠GCE=∠EDH=90°可求出△CEG≌△DHE,再通过等量代换即可解答.
解答 (1)证明:∵C、D、E分别是AP、PB、AB的中点,
∴CE=AE-AC=$\frac{1}{2}$AB-$\frac{1}{2}$AP=$\frac{1}{2}$(AB-AP)=$\frac{1}{2}$BP=DP,
∴CE+EP=DP+EP,
即CP=DE,
∵四边形CPFG和四边形PDHK都是正方形,
∴CP=CG,
∴GC=ED;
(2)证明:∵四边形CPFG和四边形PDHK都是正方形,
∴CE=DP=DH,CG=CP=DE,∠GCE=∠EDH=90°,
∴在△CEG和△DHE中,
$\left\{\begin{array}{l}{CE=DH}\\{∠GCE=EDH}\\{CG=DE}\end{array}\right.$,
∴△CEG≌△DHE(SAS).
∴EG=HE,∠EGC=∠HED
而∠EGC+∠CEG=90°,
∴∠HED+∠CEG=90°.
∴∠GEH=90°.
又∵EG=HE,
∴△EHG是等腰直角三角形.
(3)解:△EHG还是等腰直角三角形.
理由如下:
连接CE、ED,
∵点C、D、E分别是AP、PB及AB的中点,
∴CE∥PB,DE∥AP,
∴四边形CEDP是平行四边形,
∴∠PCE=∠PDE.
∴∠GCE=∠EDH,
∵CE=$\frac{1}{2}$BP=DP=DH,CG=CP=$\frac{1}{2}$AP=DE,
∴在△CEG和△DHE中,
$\left\{\begin{array}{l}{CE=DH}\\{∠GCE=EDH}\\{CG=DE}\end{array}\right.$,
∴△CEG≌△DHE(SAS),
∴EG=HE,∠EGC=∠HED.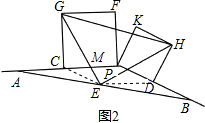
如图,设EG和CP相交于M,
则∠GEH=∠GED-∠HED
=∠GMP-∠EGC
=∠GCM
=90°,
∴△EHG是等腰直角三角形.
点评 此题属于四边形的综合题.考查了平行四边形的判定与性质、正方形的性质、全等三角形的判定与性质以及等腰直角三角形判定等知识.注意能证得△CEG≌△DHE(SAS)是关键.

 名校课堂系列答案
名校课堂系列答案
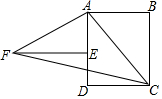 如图,四边形ABCD为长方形,△ABC旋转后能与△AEF重合,旋转中心是点A;旋转了多少度90°;连结FC,则△AFC是等腰直角三角形.
如图,四边形ABCD为长方形,△ABC旋转后能与△AEF重合,旋转中心是点A;旋转了多少度90°;连结FC,则△AFC是等腰直角三角形. 已知如图,直线l1:y=-$\frac{1}{2}$x+4与x轴、y轴分别交于点A、点B,另一直线l2:y=kx+b(k≠0)经过点C(4,0),且把△AOB分成两部分.
已知如图,直线l1:y=-$\frac{1}{2}$x+4与x轴、y轴分别交于点A、点B,另一直线l2:y=kx+b(k≠0)经过点C(4,0),且把△AOB分成两部分.