题目内容
3. 已知如图,直线l1:y=-$\frac{1}{2}$x+4与x轴、y轴分别交于点A、点B,另一直线l2:y=kx+b(k≠0)经过点C(4,0),且把△AOB分成两部分.
已知如图,直线l1:y=-$\frac{1}{2}$x+4与x轴、y轴分别交于点A、点B,另一直线l2:y=kx+b(k≠0)经过点C(4,0),且把△AOB分成两部分.(1)若l1∥l2,求过点C的直线的解析式.
(2)若△AOB被直线l2分成的两部分面积相等,求过点C的直线的解析式.
分析 (1)当l1∥l2时,k=-$\frac{1}{2}$,然后将C(4,0)代入l2的解析式中即可求出b的值.
(2)容易求得C((4,0),且C是OA的中点,所以直线l2是△AOB的中线,从而求出C的直线解析式.
解答 解:(1)由题意可知:k=-$\frac{1}{2}$
∴直线的解析式为:y=-$\frac{1}{2}$x+b
把(4,0)代入上式,
∴b=2
∴直线的解析式为:y=-$\frac{1}{2}$x+2
(2)令y=0代入y=-$\frac{1}{2}$x+4,
∴x=8,
∴点A(8,0)
令x=0代入y=-$\frac{1}{2}$x+4,
y=4,
∴B(0,4)
∴C是OA的中点
若△AOB被直线l2分成的两部分面积相等,
则直线l2与△AOB的中线重合,
即直线l2过点B
把(0,4)和(4,0)代入y=kx+b,
∴$\left\{\begin{array}{l}{b=4}\\{0=4k+b}\end{array}\right.$
解得:$\left\{\begin{array}{l}{k=-1}\\{b=4}\end{array}\right.$
∴直线l2的解析式为:y=-x+4
点评 本题考查待定系数法求解析式,解题的关键是找出相关的点坐标,然后列出方程组求出k与b的值,本题属于基础题型.

练习册系列答案
相关题目

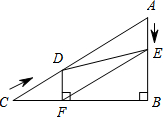 如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF.
如图,在Rt△ABC中,∠B=90°,AC=60cm,∠A=60°,点D从点C出发沿CA方向以4cm/s的速度向点A匀速运动,同时点E从点A出发沿AB方向以2cm/s的速度向点B匀速运动,当其中一个点到达终点时,另一个点也随之停止运动.设点D、E运动的时间是ts.过点D作DF⊥BC于点F,连接DE、EF. 如图所示,圆柱形玻璃容器,高8cm,底面周长为30cm,在外侧下底的点A处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口外侧的点B处有食物,蚂蚁要吃到食物所走的最短路线长度是17cm.
如图所示,圆柱形玻璃容器,高8cm,底面周长为30cm,在外侧下底的点A处有一只蚂蚁,与蚂蚁相对的圆柱形容器的上口外侧的点B处有食物,蚂蚁要吃到食物所走的最短路线长度是17cm.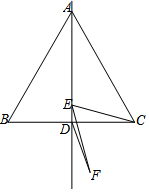 如图,已知等边△ABC边长为8 cm,D为BC中点,E为直线AD上一动点,将EC绕着点E顺时针旋转60°得到线段EF,连接DF,则线段DF最小值为2.
如图,已知等边△ABC边长为8 cm,D为BC中点,E为直线AD上一动点,将EC绕着点E顺时针旋转60°得到线段EF,连接DF,则线段DF最小值为2.