题目内容
10．
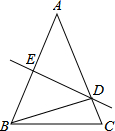已知：如图，△ABC中，AB=AC，∠A=40°，AB的中垂线交AC于点D，交AB于点E，则∠C=70°，∠DBC=30°．
分析 根据垂直平分线性质推出AD=BD，推出∠A=∠ABD=40°，根据三角形内角和定理求出∠C和∠ABC，即可得出答案．
解答 解：∵AB的垂直平分线DE，
∴AD=BD，
∴∠A=∠ABD=40°，
∵AB═AC，∠A=40°，
∴∠C=∠ABC=$\frac{1}{2}×$（180°-∠A）=70°，
∴∠DBC=∠ABC-∠ABD=30°，
故答案为：70°，30°．
点评 本题考查了三角形内角和定理，垂直平分线性质，等腰三角形的性质的应用，能推出AD=BD是解此题的关键，注意：线段垂直平分线上的点到线段两个端点的距离相等．
练习册系列答案
名校课堂系列答案
相关题目
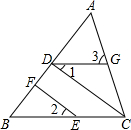如图，在△ABC中，CD⊥AB，垂足为D，点E在BC上，EF⊥AB，垂足为F．
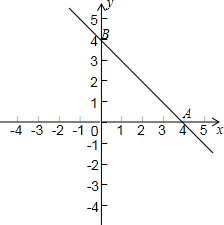右图是直线y=-x+4在平面直角坐标系中的函数图象，与x轴和y轴的交点分别为点A（4，0）和点B（0，4）．
如图，?ABCD中，AE⊥BC于E，AF⊥CD于F．若AE=2，AF=3，?ABCD的周长为25，则?ABCD的面积为15．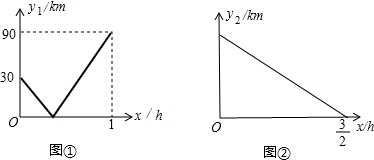
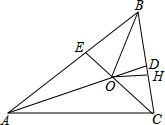已知：如图，在△ABC中，∠BAC、∠BCA的角平分线AD、CE相交于点O．OH⊥BC于点H，连接OB．