题目内容
20.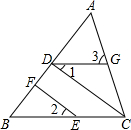 如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.
如图,在△ABC中,CD⊥AB,垂足为D,点E在BC上,EF⊥AB,垂足为F.(1)CD与EF平行吗?为什么?
(2)如果∠1=∠2,且∠3=60°,求∠ACB的度数.
分析 (1)根据垂直得出∠CDB=∠EFB=90°,根据平行线的判定得出即可;
(2)根据平行线的性质得出∠2=∠BCD,求出∠1=∠BCD,根据平行线的判定得出DG∥BC,根据平行线的性质得出即可.
解答 (1)证明:∵CD⊥AB,EF⊥AB,
∴∠CDB=∠EFB=90°,
∴CD∥EF;
(2)解:∵CD∥EF,
∴∠2=∠BCD,
∵∠1=∠2,
∴∠1=∠BCD,
∴DG∥BC,
∴∠3=∠ACB=60°.
点评 本题考查了平行线的性质和判定的应用,能正确运用平行线的性质和判定定理进行推理是解此题的关键,难度适中.

练习册系列答案
 互动课堂系列答案
互动课堂系列答案 激活思维智能训练课时导学练系列答案
激活思维智能训练课时导学练系列答案
相关题目
9.已知菱形的周长为16,有一个内角为60°,则菱形的面积为( )
| A. | $8\sqrt{3}$ | B. | $6\sqrt{3}$ | C. | $4\sqrt{3}$ | D. | $2\sqrt{3}$ |
 如图是几个小正方块所搭成几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,请画出相应的几何体的主视图和左视图.
如图是几个小正方块所搭成几何体的俯视图,小正方形中的数字表示该位置小立方块的个数,请画出相应的几何体的主视图和左视图.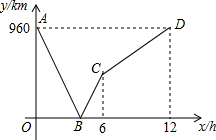 一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题:
一列快车从甲地驶往乙地,一列慢车从乙地驶往甲地,两车同时出发.设慢车行驶的时间为x(h),两车之间的距离为y(km),图中的折线表示y与x之间的函数关系.根据题中所给信息解答以下问题: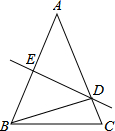 已知:如图,△ABC中,AB=AC,∠A=40°,AB的中垂线交AC于点D,交AB于点E,则∠C=70°,∠DBC=30°.
已知:如图,△ABC中,AB=AC,∠A=40°,AB的中垂线交AC于点D,交AB于点E,则∠C=70°,∠DBC=30°.