题目内容
19. 如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.
如图,把矩形纸片ABCD沿EF折叠,使点B落在边AD上的点B′处,点A落在点A′处.(1)求证:B′E=BF;
(2)若AE=3,AB=4,求BF的长.
分析 (1)根据折叠的性质以及平行线的性质可以证明∠B'FE=∠B'EF,根据等角对等边证明B'E=B'F,然后根据折叠的性质可证得;
(2)直角△A'B'E中利用勾股定理求得B'E的长,然后根据(1)的结论即可求解.
解答 (1)证明:∵矩形ABCD中,AD∥BC,
∴∠B'EF=∠EFB,
又∵∠B'FE=∠EFB,
∴∠B'FE=∠B'EF,
∴B'E=B'F,
又∵BF=B'F,
∴B'E=BF;
(2)解:∵直角△A'B'E中,A'B'=AB=4,
∴B'E=$\sqrt{A′B{′}^{2}+{A′E}^{2}}$=$\sqrt{{3}^{2}+{4}^{2}}$=5,
∴BF=N'E=5.
点评 本题考查了折叠的性质以及勾股定理,在折叠的过程中认识到相等的角和相等的边是关键.

练习册系列答案
相关题目
4.已知一次函数y=kx-1,若y随x的增大而增大,则它的图象经过哪个象限( )
| A. | 一、二、三 | B. | 一、三、四 | C. | 一、二、四 | D. | 二、三、四 |
8.下列图案中,既是中心对称图形又是轴对称图形的是( )
| A. |  | B. |  | C. |  | D. |  |

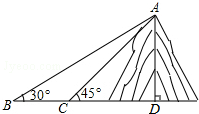 如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD是多少?(结果保留整数,测角仪忽略不计,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.73)
如图,小明在一块平地上测山高,先在B处测得山顶A的仰角为30°,然后向山脚直行100米到达C处,再测得山顶A的仰角为45°,求山高AD是多少?(结果保留整数,测角仪忽略不计,参考数据$\sqrt{2}$≈1.414,$\sqrt{3}$≈1.73)