题目内容
15. 函数y=kx+b的图象如图所示,试证明:关于x的一元二次方程x2+3x+k-1=0必有两个不等实根.
函数y=kx+b的图象如图所示,试证明:关于x的一元二次方程x2+3x+k-1=0必有两个不等实根.
分析 先根据函数y=kx+b的图象可得;k<0,再根据一元二次方程x2+3x+k-1=0中,△=32-4×1×(k-1)=13-4k>0,即可得出答案.
解答 证明:由y=kx+b的图象可得;k<0,b>0,
∵一元二次方程x2+3x+k-1=0中,△=32-4×1×(k-1)=13-4k>0,
∴一元二次方程x2+3x+k-1=0根的存在情况是有两个不相等的实数根,
点评 此题考查了一元二次方程根的判别式,一次函数图象的性质,关键是根据函数图象判断出k的符号.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
5. 如图,∠A是⊙O的圆周角,∠A=52°,则∠BOC的度数为( )
如图,∠A是⊙O的圆周角,∠A=52°,则∠BOC的度数为( )
 如图,∠A是⊙O的圆周角,∠A=52°,则∠BOC的度数为( )
如图,∠A是⊙O的圆周角,∠A=52°,则∠BOC的度数为( )| A. | 100° | B. | 104° | C. | 102° | D. | 96° |
6.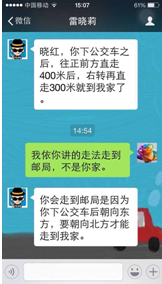 如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )
如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )
 如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )
如图为晓莉使用微信与晓红的对话纪录.据图中两个人的对话纪录,若下列有一种走法能从邮局出发走到晓莉家,此走法为( )| A. | 向北直走700米,再向西直走100米 | B. | 向北直走100米,再向东直走700米 | ||
| C. | 向北直走300米,再向西直走400米 | D. | 向北直走400米,再向东直走300米 |
4.观察图中正方形四个顶点所标的数字规律,可知数2015应标在( )

| A. | 第503个正方形的左上角 | B. | 第503个正方形的右下角 | ||
| C. | 第504个正方形的左上角 | D. | 第504个正方形的右下角 |
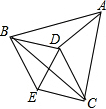 已知,如图,△ABC和△DBE中,BA=BC,BD=BE,∠ABC=∠DBE,点D是△ABC的外心,试判断四边形BDCE的形状,并说明理由.
已知,如图,△ABC和△DBE中,BA=BC,BD=BE,∠ABC=∠DBE,点D是△ABC的外心,试判断四边形BDCE的形状,并说明理由.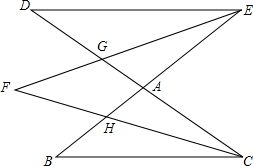 如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.
如图,DC和BE相交于点A,EF平分∠DEA,CF平分∠ACB,EF,CF分别与AD,AB交于点G,H,请猜想∠F与∠B,∠D之间的数量关系,并证明你的结论.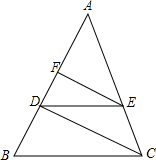 如图.在△ABC中,DE∥BC,EF∥CD.求证:AD是AB和AF的比例中项.
如图.在△ABC中,DE∥BC,EF∥CD.求证:AD是AB和AF的比例中项. 如图,在△ABC中,D是AB边上任意一点,连接CD.求证:AB+AC>DC+DB.
如图,在△ABC中,D是AB边上任意一点,连接CD.求证:AB+AC>DC+DB.