题目内容
16．
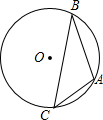已知：如图，A，B，C为⊙O上的三个点，⊙O的直径为4cm，∠ACB=45°，求AB的长．
分析 首先连接OA，OB，由∠ACB=45°，利用圆周角定理，即可求得∠AOB=90°，再利用勾股定理求解即可求得答案．
解答 
解：连接OA，OB，
∵∠ACB=45°，
∴∠AOB=2∠ACB=90°，
∵⊙O的直径为4cm，
∴OA=OB=2cm，
∴AB=$\sqrt{O{A}^{2}+O{B}^{2}}$=2$\sqrt{2}$（cm）．
点评 此题考查了圆周角定理以及勾股定理．注意准确作出辅助线是解此题的关键．
练习册系列答案
浙大优学小学年级衔接捷径浙江大学出版社系列答案
相关题目
已知：如图，C为线段AB上一点，D为AC的中点，E为BC的中点，F为DE的中点．
11．在Rt△ABC中，∠C=90°，AB=2BC，那么sinA的值为（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{\sqrt{2}}{2}$ | C． | $\frac{\sqrt{3}}{2}$ | D． | 1 |
1．我们定义一种新运算a&b（a，b是实数），规定：a&b=a2-ab-10b，等式右边是正常的实数运算，若x&2=4，则x的值为（ ）
| A． | 6或-4 | B． | -6或4 | C． | 1+$\sqrt{41}$或1-$\sqrt{41}$ | D． | 5或-4 |
8．
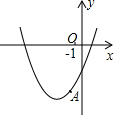如图，已知顶点为（-3，-6）的抛物线y=ax2+bx+c经过点A，点（-2，m）和（-5，n）在该抛物线上，则下列结论中不正确的是（ ）
如图，已知顶点为（-3，-6）的抛物线y=ax2+bx+c经过点A，点（-2，m）和（-5，n）在该抛物线上，则下列结论中不正确的是（ ）| A． | b2＞4ac | B． | m＞n | ||
| C． | 方程ax2+bx+c=-4的两根为-5或-1 | D． | ax2+bx+c≥-6 |
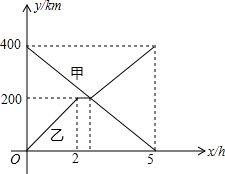甲、乙两辆汽车分别从A、B两地同时出发，沿同一条公路相向而行，乙车车发2h后休息，与甲车相遇后，继续行驶，设甲、乙两车与B地的路程分别为y甲（km），y乙（km），甲车行驶的时间为x（h），y甲，y乙与x之间的函数图象如图所示，结合图象解答下列问题：