题目内容
3.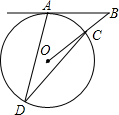 如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )
如图,在⊙O中,AD,CD是弦,连接OC并延长,交过点A的切线于点B,若∠ADC=30°,则∠ABO的度数为( )| A. | 20° | B. | 30° | C. | 40° | D. | 50° |
分析 连接AO,根据圆周角定理得到∠AOC=60°,根据切线的性质得到∠OAB=90°,根据三角形的内角和即可得到结论.
解答  解:连接AO,
解:连接AO,
∵∠ADC=30°,
∴∠AOC=60°,
∵AB是⊙O的切线,
∴∠OAB=90°,
∴∠ABO=90°-60°=30°,
故选B.
点评 本题考查了圆的切线性质、圆心角定理及解直角三角形的知识,熟记切线的性质是解题的关键.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
11.在Rt△ABC中,∠C=90°,AB=2BC,那么sinA的值为( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | 1 |
8.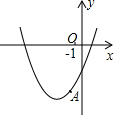 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
 如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )
如图,已知顶点为(-3,-6)的抛物线y=ax2+bx+c经过点A,点(-2,m)和(-5,n)在该抛物线上,则下列结论中不正确的是( )| A. | b2>4ac | B. | m>n | ||
| C. | 方程ax2+bx+c=-4的两根为-5或-1 | D. | ax2+bx+c≥-6 |
12.在实数0,π,$\frac{12}{11}$,-$\sqrt{4}$,$\sqrt{3}$中,是无理数的有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
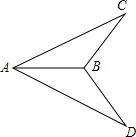 如图,已知AC=AD,∠CAB=∠DAB,求证:∠C=∠D.
如图,已知AC=AD,∠CAB=∠DAB,求证:∠C=∠D. 已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)
已知一次函数y=kx+b的图象与x轴交于点A,与y轴交于点B(0,2),且与正比例函数y=$\frac{4}{3}$x的图象交于点C(m,4)
 如图,∠B=∠E=90°,AB=a,DE=b,AC=CD,∠D=60°,∠A=30°,则BE=a+b.
如图,∠B=∠E=90°,AB=a,DE=b,AC=CD,∠D=60°,∠A=30°,则BE=a+b. 将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在C′处,BC′交AD于点E,则△EBD的形状是等腰三角形.
将一张长方形的纸片ABCD按如图所示方式折叠,使C点落在C′处,BC′交AD于点E,则△EBD的形状是等腰三角形.