题目内容
12.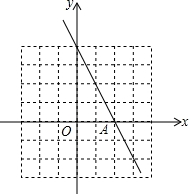 已知一次函数y1=kx+b与函数y=-2x的图象平行,且与x轴的交点A的横坐标为2.
已知一次函数y1=kx+b与函数y=-2x的图象平行,且与x轴的交点A的横坐标为2.(1)求一次函数y1=kx+b的表达式;
(2)在给定的网格中,画出函数一次函数y2=x+1的图象,并求出一次函数y1=kx+b与y=x+1图象的交点坐标;
(3)根据图象直接写出,当x取何值时,y1>y2.
分析 (1)利用两直线平行的问题得到k=-2,再把A点坐标代入y=-2x+b中求出b即可;
(2)利用描点法画出直线y=x+1,然后通过解方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-2x+4}\end{array}\right.$得到一次函数y1=kx+b与y=x+1图象的交点坐标;
(3)观察函数图象,写出直线y1=kx+b在直线y=x+1上方所对应的自变量的范围即可.
解答 解:(1)∵一次函数y1=kx+b与y=-2x的图象平行 且过A(2,0),
∴k=-2,2k+b=0,
∴b=4,
∴一次函数的表达式为y1=-2x+4;
(2)如图,

解方程组$\left\{\begin{array}{l}{y=x+1}\\{y=-2x+4}\end{array}\right.$得$\left\{\begin{array}{l}{x=1}\\{y=2}\end{array}\right.$,
所以一次函数y1=kx+b与y=x+1图象的交点坐标为(1,2);
(3)x<1.
点评 本题考查了一次函数与一元一次不等式:一次函数与一元一次不等式的关系从函数的角度看,就是寻求使一次函数y=kx+b的值大于(或小于)0的自变量x的取值范围;从函数图象的角度看,就是确定直线y=kx+b在x轴上(或下)方部分所有的点的横坐标所构成的集合.

练习册系列答案
相关题目
2.不等式4-x>0的正整数解有( )
| A. | 3个 | B. | 2个 | C. | 1个 | D. | 4个 |
3.下列各组数,不可能是一个三角形的边长的是( )
| A. | 3,4,5 | B. | 1,2,3 | C. | 4,4,6 | D. | 5,12,13 |
4.下列事件中,不可能事件是( )
| A. | 今年的除夕夜会下雪 | |
| B. | 在只装有红球的袋子里摸出一个黑球 | |
| C. | 射击运动员射击一次,命中10环 | |
| D. | 任意掷一枚硬币,正面朝上 |
 如图,已知BD,CE分别是∠ABC和∠ACB的平分线,∠DBC=∠ECB.
如图,已知BD,CE分别是∠ABC和∠ACB的平分线,∠DBC=∠ECB. 如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥y轴,交双曲线y=-$\frac{1}{x}$(x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为$\frac{3}{2}$.
如图,已知A是双曲线y=$\frac{2}{x}$(x>0)上一点,过点A作AB∥y轴,交双曲线y=-$\frac{1}{x}$(x>0)于点B,过点B作BC⊥AB交y轴于点C,连接AC,则△ABC的面积为$\frac{3}{2}$. 有一块矩形场地,如图所示,长为100米,宽为80米,要将这块地分为四块分别建成篮球、排球、足球、网球场地,若网球场地的长为篮球场地长的2倍.
有一块矩形场地,如图所示,长为100米,宽为80米,要将这块地分为四块分别建成篮球、排球、足球、网球场地,若网球场地的长为篮球场地长的2倍.